题目内容
11.先化简$\frac{{{x^2}+2x+1}}{2x-6}÷(x-\frac{1-3x}{x-3})$,并回答:原代数式的值可能等于1吗,为什么?分析 先算括号里面的,再算除法,假设代数式的值等于1,求出x的值,代入分母进行检验即可.
解答 解:不可能等于1.
原式=$\frac{(x+1)^{2}}{2(x-3)}$÷$\frac{{x}^{2}-3x-1+3x}{x-3}$
=$\frac{{(x+1)}^{2}}{2(x-3)}$•$\frac{x-3}{(x+1)(x-1)}$
=$\frac{x+1}{2(x-1)}$,
假设原代数式的值等于1,则$\frac{x+1}{2(x-1)}$=1,解得x=3,
当x=3时,原代数式无意义,
∴原代数式的值不可能等于1.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列交通标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. | . |
16.近年来某市加大了对教育经费的投入,2013年投入2500万元,2015年将投入3600万元,该市投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
| A. | 2500x2=3600 | B. | 2500(1+x)2=3600 | ||
| C. | 2500(1+x%)2=3600 | D. | 2500(1+x)+2500(1+x)2=3600 |
20.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2+2x+1=x(x+2)+1 | C. | x3-x=x(x+1)(x-1) | D. | (x+1)(x+3)=x2+4x+3 |
 如图,水以恒速(即单位时间内注入水的体积相同)注入如图的容器中,容器中水的高度h与时间t的函数关系图象可能为( )
如图,水以恒速(即单位时间内注入水的体积相同)注入如图的容器中,容器中水的高度h与时间t的函数关系图象可能为( )



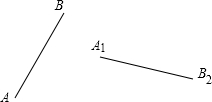 如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1(点A的对应点为A1).
如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1(点A的对应点为A1).