题目内容
18.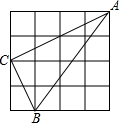 如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 设小正方形的边长为1,求出AC、BC、AB的长,利用勾股定理的逆定理证明∠ACB=90°,即可解决问题.
解答 解: 设小正方形的边长为1,
设小正方形的边长为1,
∵AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵AC2+BC2=(2$\sqrt{5}$)2+($\sqrt{5}$)2=25,AB2=52=25,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴cos∠ABC=$\frac{BC}{AB}$=$\frac{\sqrt{5}}{5}$,
故选A.
点评 本题考查勾股定理、勾股定理的逆定理、锐角三角函数等知识,解题的关键是熟练掌握勾股定理以及逆定理解决问题,属于中考常考题型.

练习册系列答案
相关题目
10. 如图,在△ABC中,∠B=90°,AB=21,BC=20,有一个半径为10的圆分别与AB、BC相切,则此圆的圆心是( )
如图,在△ABC中,∠B=90°,AB=21,BC=20,有一个半径为10的圆分别与AB、BC相切,则此圆的圆心是( )
 如图,在△ABC中,∠B=90°,AB=21,BC=20,有一个半径为10的圆分别与AB、BC相切,则此圆的圆心是( )
如图,在△ABC中,∠B=90°,AB=21,BC=20,有一个半径为10的圆分别与AB、BC相切,则此圆的圆心是( )| A. | AB边的中垂线与BC中垂线的交点 | B. | ∠B的平分线与AB的交点 | ||
| C. | ∠B的平分线与AB中垂线的交点 | D. | ∠B的平分线与BC中垂线的交点 |
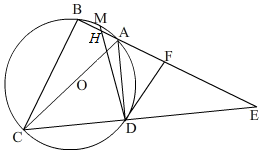 如图,⊙O是四边形ABCD的外接圆,AC是直径,分别延长AB、CD相交于点E,AC=AE,过点D作DF∥BC于点F.
如图,⊙O是四边形ABCD的外接圆,AC是直径,分别延长AB、CD相交于点E,AC=AE,过点D作DF∥BC于点F.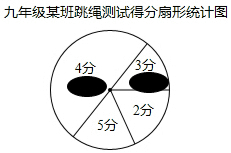 本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面扇形统计图,扇形统计图中的部分数据已被涂黑,但知道以下信息:得4分人数比得3分人数4倍多5人;得2分人数与得5分人数一样多,均为10人.
本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面扇形统计图,扇形统计图中的部分数据已被涂黑,但知道以下信息:得4分人数比得3分人数4倍多5人;得2分人数与得5分人数一样多,均为10人.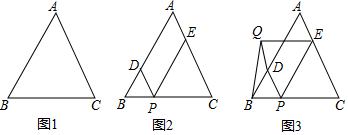
 如图,菱形花坛ABCD的边长为10m,∠BAD=120°,沿着菱形的对角线修建了两条小路AC和BD
如图,菱形花坛ABCD的边长为10m,∠BAD=120°,沿着菱形的对角线修建了两条小路AC和BD