题目内容
8. 如图,已知在⊙O中,AB=3,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
如图,已知在⊙O中,AB=3,AC是⊙O的直径,AC⊥BD于F,∠A=30°.(1)求⊙O的半径;
(2)求出图中阴影扇形OBD的面积.
分析 (1)由∠A=30°,可求得∠BOC=60°,再根据垂径定理得∠BOD=120°,求出BF以及OB的长即可;
(2)由扇形面积公式求出阴影部分的面积即可.
解答 解:(1)∵AC⊥BD于F,∠A=30°,
∴∠BOC=60°,∠OBF=30°,∠BOD=120°,
∴BF=$\frac{1}{2}$AB=$\frac{3}{2}$,
在Rt△BOF中,OB=$\frac{BF}{sin60°}$=$\frac{\frac{3}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{3}$,
即⊙O的半径为$\sqrt{3}$;
(2)图中阴影扇形OBD的面积=$\frac{120π×(\sqrt{3})^{2}}{360}$=π.
点评 本题考查了垂径定理、含30°角的直角三角形的性质、三角函数、扇形面积的计算、以及圆周角定理;熟练掌握垂径定理,由三角函数求出半径是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列图形中不是中心对称图形的为( )
| A. | 正方形 | B. | 正五边形 | C. | 正六边形 | D. | 正八边形 |
18. 如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )
如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )
 如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )
如图,O是直线AB上一点,OC⊥OD,若∠AOC=25°,则∠BOD的度数为( )| A. | 65° | B. | 115° | C. | 125° | D. | 135° |
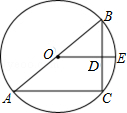 如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,求AC的长.
如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,求AC的长. 如图所示,在由边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在网格线的交点上,则∠AED的正切值等于$\frac{1}{2}$.
如图所示,在由边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在网格线的交点上,则∠AED的正切值等于$\frac{1}{2}$.
 如图,经过平移,将的顶点A移到了点D,请作出平移后图形.
如图,经过平移,将的顶点A移到了点D,请作出平移后图形.