题目内容
已知:如图①,在△AOB和△COD中,OA=OB,0C=0D,∠AOB=∠COD=50°
(1)求证:①AC=BD;②∠APB=50°
(2)如图②,在△AOB和△COD中,OA=OB,0C=OD,∠AOB=∠COD=α,则AC=BD间的等量关系为 .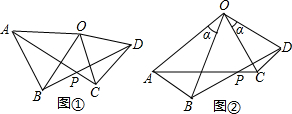
(1)求证:①AC=BD;②∠APB=50°
(2)如图②,在△AOB和△COD中,OA=OB,0C=OD,∠AOB=∠COD=α,则AC=BD间的等量关系为

考点:全等三角形的判定与性质
专题:计算题
分析:(1)①由已知角相等,利用等式的性质得到夹角相等,利用SAS得到三角形AOC与三角形BOD全等,利用全等三角形的对应边相等,对应角相等得到AC=BD,∠CAO=∠DBO;
②由三角形内角和定理及等量代换即可得证;
(2)AC=BD,∠APB=α,理由与(1)同理.
②由三角形内角和定理及等量代换即可得证;
(2)AC=BD,∠APB=α,理由与(1)同理.
解答:解:(1)①证明:∵∠AOB=∠COD=50°,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO;
②根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=50°;
(2)AC=BD,∠APB=α,理由为:
证明:∵∠AOB=∠COD=α,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=α.
故答案为:相等.
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
在△AOC和△BOD中,
|
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO;
②根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=50°;
(2)AC=BD,∠APB=α,理由为:
证明:∵∠AOB=∠COD=α,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
在△AOC和△BOD中,
|
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=α.
故答案为:相等.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为( )
如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为( )| A、30° | B、40° |
| C、46° | D、60° |
关于x的方程(a-2)x2-3x-1=0有实数根,则a满足( )
A、a≥
| ||
| B、a>-1且a≠2 | ||
C、a≥-
| ||
| D、a≠2 |
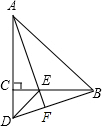 如图△ABC和△ECD都是等腰直角三角形,点C在AD上,AE的延长线交BD于点F,求证:AF⊥BD.
如图△ABC和△ECD都是等腰直角三角形,点C在AD上,AE的延长线交BD于点F,求证:AF⊥BD. 已知:如图,AB=DC,AE=BF,CE=DF,求证:AE∥BF.
已知:如图,AB=DC,AE=BF,CE=DF,求证:AE∥BF. 已知二次函数y=x2+2x+m的部分图象如下图所示,则关于x的一元二次方程x2+2x+m=0的解为
已知二次函数y=x2+2x+m的部分图象如下图所示,则关于x的一元二次方程x2+2x+m=0的解为 如图所示,有3个半圆,两两内切,且半径都在AC上,DB⊥AC,DA与小圆相交于P点,DC与中圆相交于Q点,若DB为10,则PQ=
如图所示,有3个半圆,两两内切,且半径都在AC上,DB⊥AC,DA与小圆相交于P点,DC与中圆相交于Q点,若DB为10,则PQ=