题目内容
 如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为( )
如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为( )| A、30° | B、40° |
| C、46° | D、60° |
考点:旋转的性质
专题:
分析:由旋转的性质可得:AC=AC′,∠AC′B′=∠C=70°,然后由等腰三角形的性质,求得∠AC′C的度数,继而求得答案.
解答:解:∵根据题意得:AC=AC′,∠AC′B′=∠C=70°,
∴∠AC′C=∠C=70°,
∴∠AC′B=180°-∠AC′C=110°,
∴∠B′C′B=∠AC′B-∠AC′B′=40°.
故选B.
∴∠AC′C=∠C=70°,
∴∠AC′B=180°-∠AC′C=110°,
∴∠B′C′B=∠AC′B-∠AC′B′=40°.
故选B.
点评:此题考查了旋转的性质以及等腰三角形的性质.此题难度不大,注意掌握旋转前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列长度的三条线段中,能组成三角形的是( )
| A、3cm,5cm,8cm |
| B、8cm,8cm,18cm |
| C、1cm,1cm,1cm |
| D、3cm,12cm,8cm |
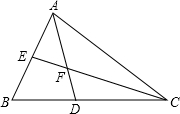 如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AD、CE交于点F,试猜想AE、CD、AC三条线段之间的数量关系,并加以证明.
如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AD、CE交于点F,试猜想AE、CD、AC三条线段之间的数量关系,并加以证明.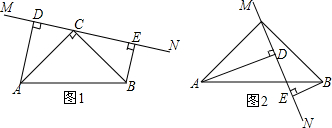
 已知:如图,AB=DC,AD=BC,O是DB的中点,过O点的直线分别交DA和BC的延长线于E,F.求证:∠E=∠F.
已知:如图,AB=DC,AD=BC,O是DB的中点,过O点的直线分别交DA和BC的延长线于E,F.求证:∠E=∠F.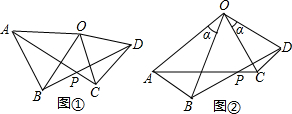
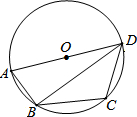 如图,ABCD是⊙O的内接四边形,AD为直径,∠C=130°,则∠ADB的度数为
如图,ABCD是⊙O的内接四边形,AD为直径,∠C=130°,则∠ADB的度数为