Question

7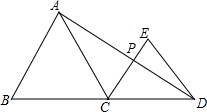．如图，如果△ABC和△CDE是直线BD同侧的两个正三角形，AD交CE于点P，BC=3，CD=1，则CP的长度为多少？

Answer 1

分析 根据等边三角形的性质得CA=CB=3，CE=DE=CD=1，∠ACB=60°，∠EDC=60°，则可判断AC∥ED，于是根据平行线分线段成比例定理得到$\frac{3}{1}$=$\frac{PC}{1-PC}$，然后根据比例性质求CP即可．

解答 解：∵△ABC和△CDE都是正三角形，
∴CA=CB=3，CE=DE=CD=1，∠ACB=60°，∠EDC=60°，
∵∠ACB=∠EDC，
∴AC∥ED，
∴$\frac{AC}{DE}$=$\frac{PC}{PE}$，即$\frac{3}{1}$=$\frac{PC}{1-PC}$，
∴PC=$\frac{3}{4}$．
答：CP的长度为$\frac{3}{4}$．

点评 本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．也考查了等边三角形的性质．