题目内容
19.当x=$\frac{1}{2-\sqrt{3}}$时,求$\sqrt{\frac{12}{1-2x+{x}^{2}}}$的值.分析 首先对x进行化简,把所求的式子进行化简,然后代入数值进行计算即可.
解答 解:x=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,
原式=$\sqrt{\frac{12}{(1-x)^{2}}}$=$\sqrt{\frac{12}{(-1-\sqrt{3})^{2}}}$=$\frac{\sqrt{12}}{1+\sqrt{3}}$=$\frac{2\sqrt{3}}{1+\sqrt{3}}$=$\frac{2\sqrt{3}(\sqrt{3}-1)}{3-1}$=$\sqrt{3}$($\sqrt{3}$-1)=3-$\sqrt{3}$.
点评 此题主要考查的是二次根式的性质以及分母有理化,注意化简$\sqrt{{a}^{2}}$,若已知x的值必须注意a的符号,根据$\sqrt{{a}^{2}}$=$\left\{\begin{array}{l}{a(a≥0)}\\{-a(a<0)}\end{array}\right.$进行化简.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
8.下列计算错误的是( )
| A. | (x+y)3+(x+y)6=(x+y)9 | B. | (x-y)3•(x-y)5=(x-y)8 | C. | (-a)2•(-a)4=a6 | D. | (-x)•(-x)5=x6 |
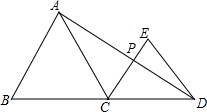 如图,如果△ABC和△CDE是直线BD同侧的两个正三角形,AD交CE于点P,BC=3,CD=1,则CP的长度为多少?
如图,如果△ABC和△CDE是直线BD同侧的两个正三角形,AD交CE于点P,BC=3,CD=1,则CP的长度为多少? 如图(图中长度单位:cm),钢管的体积是多少?
如图(图中长度单位:cm),钢管的体积是多少?