题目内容
12.我们将1×2×3×…×n记作n!(读作n的阶乘),如:2!=1×2,3!=1×2×3,4!=1×2×3×4,若设S=1×1!+2×2!+3×3!+…+2016×2016!,则S除以2017的余数是( )| A. | 0 | B. | 1 | C. | 1008 | D. | 2016 |
分析 由(n+1)!=1×2×3×…×n×(n+1)=(n+1)×n!=n×n!+n!知,可将原式两边都加上1!+2!+3!+…+2016!,即可得S=2017!-1,所以S除以2017的余数是-1,再根据2017!能被2017整除,求出S除以2017的余数是多少即可.
解答 解:∵(n+1)!=1×2×3×…×n×(n+1)=(n+1)×n!=n×n!+n!,
∴S+1!+2!+3!+…+2016!=1×1!+2×2!+3×3!+…+2016×2016!+1!+2!+3!+…+2016!,
即S+1!+2!+3!+…+2016!=1!+2!+3!+…+2017!,
则S=2017!-1,
∵2017!能被2017整除,
∴S与1的和能被2017整除,
∴S除以2017的余数是:2017-1=2016.
故选:D.
点评 本题考查规律型:数字的变化类,解答此类问题的关键是弄清新定义,得出(n+1)!=(n+1)×n!=n×n!+n!的数据变化的规律是解题的关键.

练习册系列答案
相关题目
1.an=3,am=2,a2n+3m=( )
| A. | 9 | B. | 108 | C. | 72 | D. | 17 |
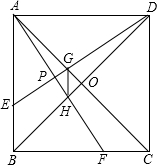 如图,已知在正方形ABCD中,AC与BD交与点O,E、F分别是AB、BC上的点,当点E、F在相同的时间、以相同的速度分别在AB、BC上从点A向B和从点B向C方向移动,是判断在E、F移动的期间:
如图,已知在正方形ABCD中,AC与BD交与点O,E、F分别是AB、BC上的点,当点E、F在相同的时间、以相同的速度分别在AB、BC上从点A向B和从点B向C方向移动,是判断在E、F移动的期间: 如图,直线AB⊥OE,则图中互余的角有两对.
如图,直线AB⊥OE,则图中互余的角有两对.