题目内容
3.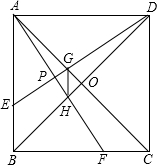 如图,已知在正方形ABCD中,AC与BD交与点O,E、F分别是AB、BC上的点,当点E、F在相同的时间、以相同的速度分别在AB、BC上从点A向B和从点B向C方向移动,是判断在E、F移动的期间:
如图,已知在正方形ABCD中,AC与BD交与点O,E、F分别是AB、BC上的点,当点E、F在相同的时间、以相同的速度分别在AB、BC上从点A向B和从点B向C方向移动,是判断在E、F移动的期间:(1)DG与AH是否保持某种不变的关系;若能请证明你的结论;若不能也请简单说明理由;
(2)判定DE与AF的位置关系,GH与DC的位置关系也仿照(1)加以讨论.
分析 (1)结论:DG=AH,且DG⊥AH.由△DAE≌△ABF,推出∠ADG=∠BAH,再证明△ADG≌△ABH,推出DG=BH,由∠BAH+∠HAD=90°,∠BAH=∠ADG,推出∠HAD+∠ADG=90°,推出∠APD=90°,即可解决问题.
(2)①结论:DE⊥AF.(1)中已经证明.②结论:GH∥CD.由△AOH≌△DOG,推出OG=OH,推出∠OGH=∠OHG=45°,由∠OCD=45°,推出∠HGO=∠OCD,推出GH∥CD即可.
解答 解:(1)结论:DG=AH,且DG⊥AH.
理由:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠ABF=90°,
在△DAE和△ABF中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAE=∠ABF}\\{AE=BF}\end{array}\right.$,
∴△DAE≌△ABF,
∴∠ADG=∠BAH,
∵∠DAG=∠ABH=45°,
在△ADG和△ABH中,
$\left\{\begin{array}{l}{∠ADG=∠BAH}\\{AD=AB}\\{∠DAG=∠ABH}\end{array}\right.$,
∴△ADG≌△ABH,
∴DG=BH,
∵∠BAH+∠HAD=90°,∠BAH=∠ADG,
∴∠HAD+∠ADG=90°,
∴∠APD=90°,
∴DG⊥AH.
(2)①结论:DE⊥AF.
理由:由(1)可知:DE⊥AF,
②结论:GH∥CD.
理由:∵∠APD=∠AOD=90°,∠AGP=∠DGO,
∴∠PAG=∠GDO,
在△AOH和△DOG中,
$\left\{\begin{array}{l}{∠OAH=∠GDO}\\{∠AOH=∠DOG}\\{AH=DG}\end{array}\right.$,
∴△AOH≌△DOG,
∴OG=OH,
∴∠OGH=∠OHG=45°,
∵∠OCD=45°,
∴∠HGO=∠OCD,
∴GH∥CD.
点评 本题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | 100° | B. | 100°或20° | C. | 100°或50° | D. | 20° |
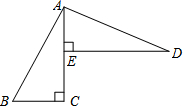 已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.
已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE. 光大路桥公司中标承包了一段路基工程,进入施工场地后,所挖路基的长度y(m)与工作时间x(天)之间的函数关系如图所示,请根据提供的信息解答下列问题:
光大路桥公司中标承包了一段路基工程,进入施工场地后,所挖路基的长度y(m)与工作时间x(天)之间的函数关系如图所示,请根据提供的信息解答下列问题: