题目内容
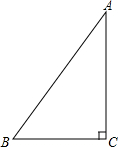 如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
考点:勾股定理,勾股定理的逆定理
专题:动点型
分析:(1)首先利用勾股定理计算出AC长,根据题意可得CP=2cm,再利用勾股定理计算出PB的长,进而可得△ABP的周长;
(2)当P在AC上运动时△BCP为直角三角形,由此可得0<t≤4;当P在AB上时,CP⊥AB时,△BCP为直角三角形,首先计算出CP的长,然后再利用勾股定理计算出AP长,进而可得答案.
(3)分类讨论:当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,t+2t-3=6;当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,t-4+2t-8=6.
(2)当P在AC上运动时△BCP为直角三角形,由此可得0<t≤4;当P在AB上时,CP⊥AB时,△BCP为直角三角形,首先计算出CP的长,然后再利用勾股定理计算出AP长,进而可得答案.
(3)分类讨论:当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,t+2t-3=6;当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,t-4+2t-8=6.
解答: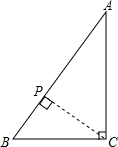 解:(1)∵∠C=90°,AB=5cm,BC=3cm,
解:(1)∵∠C=90°,AB=5cm,BC=3cm,
∴AC=4cm,动点P从点C开始,按C→B→A→C的路径运动,速度为每秒1cm,
∴出发2秒后,则CP=2cm,
∵∠C=90°,
∴PB=
=
cm,
∴△ABP的周长为:AP+PB+AB=2+5+
=7+
(cm);
(2)∵AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴P在AC上运动时△BCP为直角三角形,
∴0<t≤4,
当P在AB上时,CP⊥AB时,△BCP为直角三角形,
∵
×AB×CP=
×AC×BC,
∴
×5×CP=
×3×4,
解得:CP=
cm,
∴AP=
=
cm,
∴AC+AP=
cm,
∵速度为每秒1cm,
∴t=
,
综上所述:当0<t≤4或t=
,△BCP为直角三角形;
(3)当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t+2t-3=6,
∴t=2;
当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t-4+2t-8=6,
∴t=6,
∴当t=2或6秒时,直线PQ把△ABC的周长分成相等的两部分.
 解:(1)∵∠C=90°,AB=5cm,BC=3cm,
解:(1)∵∠C=90°,AB=5cm,BC=3cm,∴AC=4cm,动点P从点C开始,按C→B→A→C的路径运动,速度为每秒1cm,
∴出发2秒后,则CP=2cm,
∵∠C=90°,
∴PB=
| 22+32 |
| 13 |
∴△ABP的周长为:AP+PB+AB=2+5+
| 13 |
| 13 |
(2)∵AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴P在AC上运动时△BCP为直角三角形,
∴0<t≤4,
当P在AB上时,CP⊥AB时,△BCP为直角三角形,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:CP=
| 12 |
| 5 |
∴AP=
| AC2-CP2 |
| 16 |
| 5 |
∴AC+AP=
| 36 |
| 5 |
∵速度为每秒1cm,
∴t=
| 36 |
| 5 |
综上所述:当0<t≤4或t=
| 36 |
| 5 |
(3)当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t+2t-3=6,
∴t=2;
当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t-4+2t-8=6,
∴t=6,
∴当t=2或6秒时,直线PQ把△ABC的周长分成相等的两部分.
点评:此题主要考查了勾股定理以及其逆定理等知识,利用分类讨论的思想求出是解题关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
小王成公共汽车从甲地到相距50km的乙地办事,然后乘出租车返回,出租车的品均速度比公共汽车多20km/h,回来时路上所花时间比去时节省了
.设公共汽车的平均速度为x km/h,则下面列出的方程中正确的是( )
| 1 |
| 4 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图所示,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为34cm,且BC=20cm,求AB的长.
如图所示,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为34cm,且BC=20cm,求AB的长. 如图,已知?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于E.
如图,已知?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于E.