题目内容
 如图,已知?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于E.
如图,已知?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于E.(1)求证:△AOD≌△EOC;
(2)连接AC、DE,当∠B=∠AEB=
考点:平行四边形的性质,全等三角形的判定与性质,正方形的判定
专题:
分析:(1)利用平行四边形的性质以及全等三角形的判定方法(ASA),得出△AOD≌△EOC;
(2)利用等腰直角三角形的性质结合平行四边形的判定以及正方形的判定得出即可.
(2)利用等腰直角三角形的性质结合平行四边形的判定以及正方形的判定得出即可.
解答: (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADC=∠DCE,
在△AOD和△EOC中,
,
∴△AOD≌△EOC(ASA);
(2)解:当∠B=∠AEB=45°时,四边形ACED是正方形,
理由:∵∠B=∠AEB=45°,
∴AB=AE,
∵△AOD≌△EOC,
∴AD=EC,∠DAE=∠AEC=45°,
又∵AD∥EC,
∴四边形ACED是平行四边形,
则AD=BC=EC,
∴AC⊥EC,
∵△ABE是等腰直角三角形,
∴AC=EC,∠ACE=90°,
∴平行四边形ACED是正方形.
故答案为:45°.
 (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠ADC=∠DCE,
在△AOD和△EOC中,
|
∴△AOD≌△EOC(ASA);
(2)解:当∠B=∠AEB=45°时,四边形ACED是正方形,
理由:∵∠B=∠AEB=45°,
∴AB=AE,
∵△AOD≌△EOC,
∴AD=EC,∠DAE=∠AEC=45°,
又∵AD∥EC,
∴四边形ACED是平行四边形,
则AD=BC=EC,
∴AC⊥EC,
∵△ABE是等腰直角三角形,
∴AC=EC,∠ACE=90°,
∴平行四边形ACED是正方形.
故答案为:45°.
点评:此题主要考查了全等三角形的判定与性质以及正方形的判定和平行四边形的判定与性质等知识,正确利用平行四边形的判定与性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二元一次方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列运算正确的是( )
| A、a•a2=a2 |
| B、(ab)3=a3b3 |
| C、(a3)2=a5 |
| D、a8÷a2=a4 |
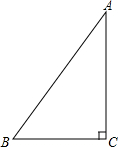 如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.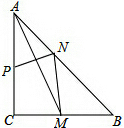 如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为( )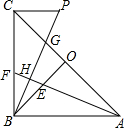 如图,等腰Rt△ABC中,O为斜边AC的中点,∠CAB的平分线分别交BO,BC于点E,F,BP⊥AF于H,PC⊥BC,AE=1,PG=
如图,等腰Rt△ABC中,O为斜边AC的中点,∠CAB的平分线分别交BO,BC于点E,F,BP⊥AF于H,PC⊥BC,AE=1,PG=