题目内容
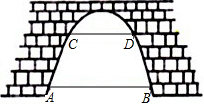 如图,有一座抛物线形拱桥,当水位正常时,水面宽度AB为12m,水位上升5m,就达到警戒水位,这时水面宽度CD为8m.
如图,有一座抛物线形拱桥,当水位正常时,水面宽度AB为12m,水位上升5m,就达到警戒水位,这时水面宽度CD为8m.(1)在图中建立平面直角坐标系,求出该抛物线的解析式.
(2)若洪水到来时,水位以每天0.6m的速度上升,求水过警戒水位CD后几天淹到桥的拱顶.
(3)在正常水位的基础上,当水位上升l(m)时,桥下水面的宽度为n(m),求出用n表示为l的函数解析式.
考点:二次函数的应用
专题:
分析:(1)根据题意建立直角坐标系,如图,设抛物线的解析式为y=ax2+c,由待定系数法求出其解即可;
(2)当x=0时,求出顶点坐标,就可以求出桥顶到警戒线的距离,进而得出结论;
(3)把坐标(
,l)代入(1)的解析式即可.
(2)当x=0时,求出顶点坐标,就可以求出桥顶到警戒线的距离,进而得出结论;
(3)把坐标(
| n |
| 2 |
解答:解:(1)如图,设抛物线的解析式为y=ax2+c,由题意,得
,
解得:
,
∴y=-0.25x2+9;
(2)当x=0时,y=9.
(9-5)÷0.6=
天.
答:水过警戒水位CD后
天淹到桥的拱顶;
(3)把坐标(
,l)代入y=-0.25x2+9,得
l=-0.25×
+9=-
n2+9.
∴l=-
n2+9.

|
解得:
|
∴y=-0.25x2+9;
(2)当x=0时,y=9.
(9-5)÷0.6=
| 20 |
| 3 |
答:水过警戒水位CD后
| 20 |
| 3 |
(3)把坐标(
| n |
| 2 |
l=-0.25×
| n2 |
| 4 |
| 1 |
| 16 |
∴l=-
| 1 |
| 16 |
点评:本题考查待定系数法求函数解析式的运用,行程问题的数量关系时间=路程÷时间的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
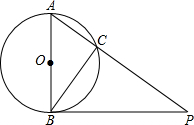 如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( )
如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( ) | A、5cm | B、2.4cm |
| C、3.6cm | D、1.8cm |
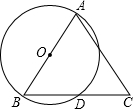 如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状:
如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状: