题目内容
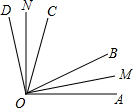如图所示，OB、OC是∠AOD内的任意两条射线，OM平分∠AOB，ON平分∠COD．若∠AOD=120°，∠BOC=70°．求∠MON使多少度？考点：角的计算,角平分线的定义
专题：
分析：根据已知条件得出∠DOC+∠BOA的度数，再根据角平分线的定义得出∠NOC+∠BOM的度数，最后根据∠MON=∠NOC+∠BOM+∠BOC，代入计算即可得出答案．
解答：解：∵∠AOD=120°，∠BOC=70°，
∴∠DOC+∠BOA=50°，
∵OM平分∠AOB，ON平分∠COD，
∴∠NOC+∠BOM=25°，
∴∠MON=∠NOC+∠BOM+∠BOC=25°+70°=95°；
答：∠MON的度数是95°．
∴∠DOC+∠BOA=50°，
∵OM平分∠AOB，ON平分∠COD，
∴∠NOC+∠BOM=25°，
∴∠MON=∠NOC+∠BOM+∠BOC=25°+70°=95°；
答：∠MON的度数是95°．
点评：此题考查了角的计算和角平分线的定义，熟练掌握角平分线的定义得出∠NOC+∠BOM=25°是本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
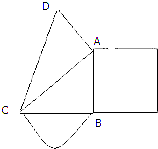如图，Rt△ABC中，以AB为边向外作正方形，以BC为直径向外作半圆，且正方形面积与半圆面积之比为9：2π，现已AC为直角边向外作Rt△ACD，若AD=8，CD=17，则正方形的面积为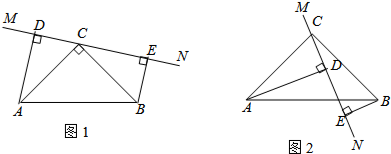
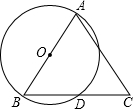如图，AB是⊙O的直径，D是⊙O上的任意一点（不与点A、B重合），延长BD到点C，使DC=BD，判断△ABC的形状：
如图，在△ABC中，两条中线AD、BE交于点F，则S△EDF：S△ABC=