题目内容
方程3x=12的解有___个,不等式3x<12的解有____个.
 1 无数
【解析】解方程3x=12,可得x=4,所以方程只有一个解,解不等式3x<12,可得x<4,知不等式的解有无数个.
故答案为:1;无数.
1 无数
【解析】解方程3x=12,可得x=4,所以方程只有一个解,解不等式3x<12,可得x<4,知不等式的解有无数个.
故答案为:1;无数.
练习册系列答案
相关题目
(2016四川省泸州市)某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
 (1)A种商品的单价为16元、B种商品的单价为4元;(2)有两种方案:方案(1):m=12,2m﹣4=20 即购买A商品的件数为12件,则购买B商品的件数为20件;方案(2):m=13,2m﹣4=22 即购买A商品的件数为13件,则购买B商品的件数为22件.
【解析】试题分析:(1)、设A种商品的单价为x元、B种商品的单价为y元,根据题意得出方程组,从而求出x和y的值;(2)、设购买A商品的...
(1)A种商品的单价为16元、B种商品的单价为4元;(2)有两种方案:方案(1):m=12,2m﹣4=20 即购买A商品的件数为12件,则购买B商品的件数为20件;方案(2):m=13,2m﹣4=22 即购买A商品的件数为13件,则购买B商品的件数为22件.
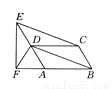
【解析】试题分析:(1)、设A种商品的单价为x元、B种商品的单价为y元,根据题意得出方程组,从而求出x和y的值;(2)、设购买A商品的... 如图所示,在 ABCD中,CE∥BD,EF⊥AB交BA延长线于点F,E,D,A在一条直线上,那么有DF=
ABCD中,CE∥BD,EF⊥AB交BA延长线于点F,E,D,A在一条直线上,那么有DF=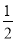 AE,请你说明理由.(提示:直角三角形中斜边中线等于斜边的一半)
AE,请你说明理由.(提示:直角三角形中斜边中线等于斜边的一半)
 答案见解析
【解析】试题分析:首先根据平行四边形的性质可得AD=BC,AD∥BC,再证明四边形EDBC是平行四边形,可得ED=CB,然后根据直角三角形斜边上的中线等于斜边的一半可得结论.
试题解析:证明:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∵CE∥BD,∴四边形EDBC是平行四边形,∴ED=CB,∴ED=AD.∵EF⊥AB,∴△EFA是直角三角形,∴DF=AE.
答案见解析
【解析】试题分析:首先根据平行四边形的性质可得AD=BC,AD∥BC,再证明四边形EDBC是平行四边形,可得ED=CB,然后根据直角三角形斜边上的中线等于斜边的一半可得结论.
试题解析:证明:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∵CE∥BD,∴四边形EDBC是平行四边形,∴ED=CB,∴ED=AD.∵EF⊥AB,∴△EFA是直角三角形,∴DF=AE. A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( )
A. 3种 B 4种 C 5种 D 6种
 B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法.
B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法. 已知(b+2)xb+1<-3是关于x的一元一次不等式,试求b的值,并解这个一元一次不等式.
 x<-1.5.
【解析】试题分析:先根据一元一次不等式的概念,知b+1=0,求得b,然后代入解不等式即可.
试题解析:∵(b+2)xb+1<-3是关于x的一元一次不等式,
∴b+1=1,则b=0,
∴2x<-3,
解得x<-1.5.
x<-1.5.
【解析】试题分析:先根据一元一次不等式的概念,知b+1=0,求得b,然后代入解不等式即可.
试题解析:∵(b+2)xb+1<-3是关于x的一元一次不等式,
∴b+1=1,则b=0,
∴2x<-3,
解得x<-1.5. 若a是不等式2x﹣1>5的解,b不是不等式2x﹣1>5的解,则下列结论正确的是( )
A. a>b B. a≥b C. a<b D. a≤b
 A
【解析】解2x﹣1>5得x>3,.
a是不等式2x﹣1>5的解则a>3,b不是不等式2x﹣1>5的解,则b≤3.
故a>b.
故选A.
A
【解析】解2x﹣1>5得x>3,.
a是不等式2x﹣1>5的解则a>3,b不是不等式2x﹣1>5的解,则b≤3.
故a>b.
故选A. 若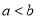 ,则下列各式中一定成立的是( )
,则下列各式中一定成立的是( )
A. 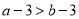 B.
B. 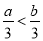 C.
C. 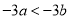 D.
D. 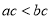
 B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A.
B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A. 如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为( )
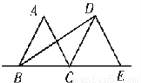
A. 18 B. 3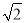 C. 12 D. 2
C. 12 D. 2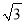
 D
【解析】过点D作DF⊥EC于点F,利用正三角形的性质得出CF=1,BF=3,再利用勾股定理求出DF==,则可得BD=.
故选:D.
D
【解析】过点D作DF⊥EC于点F,利用正三角形的性质得出CF=1,BF=3,再利用勾股定理求出DF==,则可得BD=.
故选:D. 如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=__度.
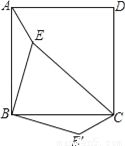
 135
【解析】试题分析:首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,∴△EBE′是直角三角形,
∵△ABE与△CE′B全等
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
...
135
【解析】试题分析:首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,∴△EBE′是直角三角形,
∵△ABE与△CE′B全等
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
... 
