题目内容
1.已知4x2-2ax-3+2a=0无实根,且a是实数.化简$\sqrt{4{a}^{2}-12a+9}$+$\sqrt{{a}^{2}-12a+36}$.分析 根据判别式的意义得到(-2a)2-4×4(-3+2a)<0,解得2<a<6,再根据二次根式的性质化简原式得到原式=|2a-3|+|a-6|,然后根据a的范围去绝对值后合并即可.
解答 解:∵4x2-2ax-3+2a=0无实根,
∴△=(-2a)2-4×4(-3+2a)<0,
∴2<a<6,
∴$\sqrt{4{a}^{2}-12a+9}$+$\sqrt{{a}^{2}-12a+36}$=$\sqrt{(2a-3)^{2}}$+$\sqrt{(a-6)^{2}}$
=|2a-3|+|a-6|
=2a-3+6-a
=a+3.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了二次根式的性质.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
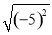 的结果是( )
的结果是( )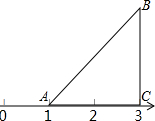 如图,等腰直角三角形ABC的直角边AC落在数轴上,点A表示的数是1,点C表示的数是3,以A为旋转中心逆时针旋转△ABC.
如图,等腰直角三角形ABC的直角边AC落在数轴上,点A表示的数是1,点C表示的数是3,以A为旋转中心逆时针旋转△ABC.