题目内容
15.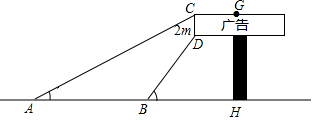 数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长($\sqrt{3}≈1.73$,要求结果精确得到0.1m)
数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长($\sqrt{3}≈1.73$,要求结果精确得到0.1m)
分析 首先过点D作DE⊥AH于点E,设DE=xm,则CE=(x+2)m,解Rt△AEC和Rt△BED,得出AE=$\sqrt{3}$(x+2),BE=$\frac{\sqrt{3}}{3}$x,根据AE-BE=10列出方程$\sqrt{3}$(x+2)-$\frac{\sqrt{3}}{3}$x=10,解方程求出x的值,进而得出GH的长.
解答  解:如图,过点D作DE⊥AH于点E,设DE=xm,则CE=(x+2)m.
解:如图,过点D作DE⊥AH于点E,设DE=xm,则CE=(x+2)m.
在Rt△AEC和Rt△BED中,有tan30°=$\frac{CE}{AE}$,
tan60°=$\frac{DE}{BE}$,
∴AE=$\sqrt{3}$(x+2),BE=$\frac{\sqrt{3}}{3}$x,
∵AE-BE=AB=10,
∴$\sqrt{3}$(x+2)-$\frac{\sqrt{3}}{3}$x=10,
∴x=5$\sqrt{3}$-3,
∴GH=CD+DE=2+5$\sqrt{3}$-3=5$\sqrt{3}$-1≈7.7(m).
答:GH的长约为7.7m.
点评 此题主要考查了解直角三角形的应用-仰角俯角问题,根据已知构造直角三角形得出DE的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
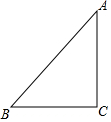 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)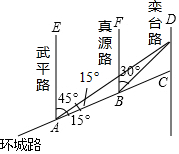 如图,AC是某市环城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量东方家具城D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°,求C、D之间的距离(结果保留根号).
如图,AC是某市环城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量东方家具城D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°,求C、D之间的距离(结果保留根号).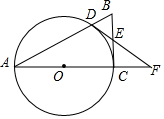 如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.