题目内容
5.先化简,再求代数式$\frac{x}{x+2}$-$\frac{1}{x-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$的值,其中x=$\sqrt{3}$-2.分析 根据分式的除法和减法可以化简题目中的式子,然后将x=$\sqrt{3}$-2代入化简后的式子即可解答本题.
解答 解:$\frac{x}{x+2}$-$\frac{1}{x-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$
=$\frac{x}{x+2}-\frac{1}{x-1}•\frac{(x-1)^{2}}{x+2}$
=$\frac{x}{x+2}-\frac{x-1}{x+2}$
=$\frac{1}{x+2}$,
当x=$\sqrt{3}$-2时,原式=$\frac{1}{\sqrt{3}-2+2}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式的化简求值的方法.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,平行四边形ABCD的对角线相交于O点,则图中有4对全等三角形.
如图,平行四边形ABCD的对角线相交于O点,则图中有4对全等三角形. 如图,在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=7,则点D到斜边AB的距离为7.
如图,在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=7,则点D到斜边AB的距离为7.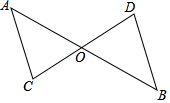 如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.
如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD. 如图,直线a∥b,直线l与直线a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于51°.
如图,直线a∥b,直线l与直线a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于51°.