题目内容
18.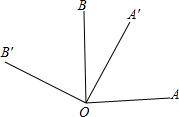 如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.
如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.(1)试说明∠AOA′与∠BOB′的大小关系;
(2)若∠AOB=90°,且∠A′OB=32°,求∠AOB′的度数;
(3)若∠AOB′=160°,且∠A′OB:∠BOB′=2:3,求θ角的度数.
分析 (1)首先根据题意,可得∠AOB=∠A′OB′,所以∠AOB-∠A′OB=∠A′OB′-∠A′OB,据此判断出∠AOA′=∠BOB′即可.
(2)首先根据∠AOB=90°,可得∠A′OB′=90°;然后根据余角的性质,求出∠AOA′的度数,再用∠AOA′的度数加上90°,求出∠AOB′的度数是多少即可.
(3)首先根据∠A′OB:∠BOB′=2:3,∠AOA′=∠BOB′,可得∠A′OB:∠AOA′=2:3;然后根据∠AOB′=160°,求出∠BOB′的度数,即可求出θ角的度数.
解答 解:(1)∵把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′,
∴∠AOB=∠A′OB′,
∴∠AOB-∠A′OB=∠A′OB′-∠A′OB,
即∠AOA′=∠BOB′.
(2)∵∠AOB=90°,∠AOB=∠A′OB′
∴∠A′OB′=90°,
∵∠AOB=90°,∠A′OB=32°,
∴∠AOA′=90°-32°=58°,
∴∠AOB′=∠AOA′+∠A′OB′=58°+90°=148°,
即∠AOB′的度数是148°.
(3)∵∠A′OB:∠BOB′=2:3,∠AOA′=∠BOB′,
∴∠A′OB:∠AOA′=2:3,
∴∠A′OB:∠BOB′:∠AOA′=2:3:3,
又∵∠AOB′=160°,
∴θ=∠AOA′=∠BOB′=160°×$\frac{3}{2+3+3}$=160$°×\frac{3}{8}$=60°,
即θ角的度数是60°.
点评 此题主要考查了角的计算,要熟练掌握,解答此题的关键是要明确旋转的性质和应用,以及余角的性质和应用.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3.若等腰三角形的两边的长是方程x2-20x+91=0的两个根,则此三角形周长为( )
| A. | 27 | B. | 33 | C. | 27和33 | D. | 21 |
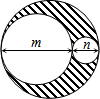 三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大的圆的直径,则图中阴影部分的面积是$\frac{π}{2}$mn.
三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大的圆的直径,则图中阴影部分的面积是$\frac{π}{2}$mn.