题目内容
3.若等腰三角形的两边的长是方程x2-20x+91=0的两个根,则此三角形周长为( )| A. | 27 | B. | 33 | C. | 27和33 | D. | 21 |
分析 先求出方程的解,根据等腰三角形的性质得出两种情况,求出每种情况的三角形的周长即可.
解答 解:x2-20x+91=0,
(x-7)(x-13)=0,
x-7=0,x-13=0,
x1=7,x2=13,
当三角形的三边长为7,7,13时,符合三角形的三边关系定理,三角形的周长为7+7+13=27;
当三角形的三边长为7,13,13时,符合三角形的三边关系定理,三角形的周长为7+13+13=33;
故选C.
点评 本题考查了解一元二次方程,等腰三角形的性质,三角形的三边关系定理的应用,解此题的关键是能求出符合条件的所有情况,难度适中.

练习册系列答案
相关题目
14.数据0.000065用科学记数法表示为( )
| A. | 65×10-5 | B. | 6.5×10-5 | C. | 6.5×10-6 | D. | 6.5×10-5 |
8.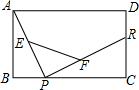 如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
 如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )| A. | 线段EF的长逐渐增大 | B. | 线段EF的长逐渐减少 | ||
| C. | 线段EF的长不变 | D. | 线段EF的长先增大后变小 |
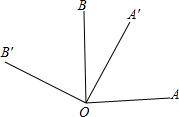 如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.
如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′. 如图,已知AB∥CD,EF与AB,CD相交于点M,N,∠AMR=∠CNP,请你猜想MR与NP的位置关系?并说明理由.
如图,已知AB∥CD,EF与AB,CD相交于点M,N,∠AMR=∠CNP,请你猜想MR与NP的位置关系?并说明理由.