题目内容
13.已知方程4x2-2(m+1)x+m=0的两个根恰好是一个直角三角形的两锐角的余弦,求m的值.分析 设直角三角形的两锐角分别为α,β,根据根与系数的关系表示出两根之和与两根之积,利用同角三角函数间的基本关系变形,再利用完全平方公式化简,得到关于m的方程,求出方程的解即可得到m的值.
解答 解:设直角三角形的两锐角分别为α,β,
根据题意得:方程4x2-2(m+1)x+m=0的两根为cosα与cosβ(sinα=cosβ),
∴cosα+cosβ=cosα+sinβ=-$\frac{-2(m+1)}{4}$,cosαsinβ=$\frac{m}{4}$>0,
又sin2α+cos2β=1,
∴(cosα+sinβ)2-2sinαcosβ=$\frac{(m+1)^{2}}{4}$-$\frac{m}{2}$=1,
整理得:m2=3,
解得:m=$\sqrt{3}$或m=-$\sqrt{3}$(舍去),
则m的值为$\sqrt{3}$.
点评 此题考查了一元二次方程根与系数的关系,以及互余两角三角函数的关系,熟练掌握根与系数的关系是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.函数y=$\frac{\sqrt{x+2}}{2-x}$中,自变量x的取值范围是( )
| A. | x≥-2且x≠2 | B. | x≥-2 | C. | x≠0 | D. | x<2 |
5.一组数据:1,x,2,3,0,平均数是2,则方差是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 10 |
3. 如图,AB⊥CD于点O,直线EF过点O,若∠AOE=65°,则∠DOF度数为( )
如图,AB⊥CD于点O,直线EF过点O,若∠AOE=65°,则∠DOF度数为( )
 如图,AB⊥CD于点O,直线EF过点O,若∠AOE=65°,则∠DOF度数为( )
如图,AB⊥CD于点O,直线EF过点O,若∠AOE=65°,则∠DOF度数为( )| A. | 35° | B. | 25° | C. | 15° | D. | 10° |
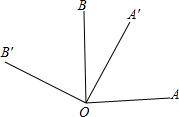 如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.
如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.