题目内容
10.设a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2-1)=12,则这个直角三角形的斜边长为2.分析 此题实际上求$\sqrt{{a}^{2}+{b}^{2}}$的值.设t=a2+b2,将原方程转化为关于t的一元二次方程t(t-1)=12,通过解方程求得t的值即可.
解答 解:设t=a2+b2,则由原方程,得
t(t-1)=12,
整理,得
(t-4)(t+3)=0,
解得t=4或t=-3(舍去).
则a2+b2=4,
∵a,b是一个直角三角形两条直角边的长,
∴这个直角三角形的斜边长为$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{4}$=2.
故答案是:2.
点评 此题考查了换元法解一元二次方程,以及勾股定理,熟练运用勾股定理是解本题的关键.

练习册系列答案
相关题目
5.一组数据:1,x,2,3,0,平均数是2,则方差是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 10 |
19. 下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )
下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )
 下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )
下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )| A. | + | B. | +++ | C. |  | D. |  |
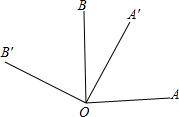 如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.
如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.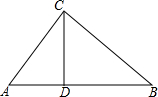 △ABC中,AB=17,AC=10,AB边上的高CD=8,求BC的长.
△ABC中,AB=17,AC=10,AB边上的高CD=8,求BC的长.