题目内容
9.请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.A.已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE与对角线AC相交于点M,则$\frac{MC}{AM}$的值是$\frac{8}{5}$或$\frac{8}{11}$.
B.用科学计算器计算:$\sqrt{7}$sin69°≈2.47(精确到0.01).
分析 A、分类讨论:当点E在线段AE上,如图1,根据菱形的性质得BC=AD=8,BC∥AD,则AE=5,利用BC∥AM,根据平行线分线段成比例定理得到$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{8}{5}$;当点E在线段AE的延长线上,如图2,则AE=11,同理可得$\frac{MC}{AM}$=$\frac{8}{11}$;
B、直接使用科学计算器进行计算.
解答 解:A、当点E在线段AE上,如图1,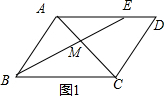
∵菱形ABCD的边长是8,
∴BC=AD=8,BC∥AD,
∵DE=3,
∴AE=5,
∵BC∥AM,
∴$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{8}{5}$;
当点E在线段AE的延长线上,如图2,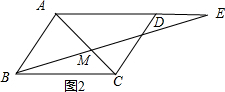 则AE=11,
则AE=11,
∵BC∥AM,
∴$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{8}{11}$,
即$\frac{MC}{AM}$的值为$\frac{8}{5}$或$\frac{8}{11}$;
B、$\sqrt{7}$sin69°≈2.47(精确到0.01).
故答案为$\frac{8}{5}$或$\frac{8}{11}$; 2.47.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了平行线分线段成比例定理和计算器的使用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
14.数据0.000065用科学记数法表示为( )
| A. | 65×10-5 | B. | 6.5×10-5 | C. | 6.5×10-6 | D. | 6.5×10-5 |
19. 下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )
下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )
 下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )
下列基本图形经过平移,旋转成轴对称变换后不能得到下图的是( )| A. | + | B. | +++ | C. |  | D. |  |
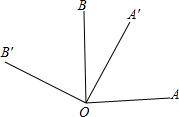 如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.
如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.