题目内容
3.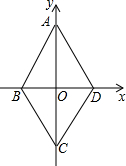 如图,四边形ABCD是周长为20cm的菱形,点A的坐标是(0,4),则点B的坐标为(-3,0).
如图,四边形ABCD是周长为20cm的菱形,点A的坐标是(0,4),则点B的坐标为(-3,0).
分析 本题可根据菱形的四边相等的性质以及菱形的周长可求出边长的值,再根据勾股定理即可求出OB的长,进而可求出点B的坐标.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵菱形ABCD是周长为20,
∴AB=$\frac{1}{4}$×20=5,
∵点A的坐标是(0,4),
∴AO=4,
∴BO=$\sqrt{{5}^{2}-{4}^{2}}=3$,
∴点B的坐标为(-3,0),
故答案为:(-3,0).
点评 本题考查了菱形的性质、坐标与图形的性质以及勾股定理.在直角坐标系中,运用菱形的性质,四边相等,对角线互相垂直平分,根据点的坐标确定相关线段的长度,运用勾股定理求解.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
13.如果线段a,b,c能组成直角三角形,则它们的比可以是( )
| A. | 1:2:4 | B. | 1:3:5 | C. | 6:4:7 | D. | 5:12:13 |
14.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在一分钟内踢100个以上(含100个)为优秀.如表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
经统计发现甲、乙两班总个数相同,方差分别为46.8,103.2(平方个).试从中位数,方差,优秀率三个方面考虑,哪个班为冠军?
| 1号 | 2号 | 3号 | 4号 | 5号 | 总个数 | |
| 甲班 | 89 | 100 | 98 | 110 | 103 | 500 |
| 乙班 | 100 | 89 | 97 | 119 | 95 | 500 |
18.已知直线y=kx(x≠0)经过点(-1,2),则此正比例函数的解析式为( )
| A. | y=-2x | B. | y=2x | C. | y=-$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
 如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D.
如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D. 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
 如图,在△ABC中,AB=AC,BD⊥AC于点D,∠A=40°,则∠CBD的度数为20°.
如图,在△ABC中,AB=AC,BD⊥AC于点D,∠A=40°,则∠CBD的度数为20°.