题目内容
5.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为( )| A. | y=$\frac{12}{x}$ | B. | y=-$\frac{12}{x}$ | C. | y=$\frac{15}{x}$ | D. | y=-$\frac{15}{x}$ |
分析 过P作PD⊥x轴于D,则PD=3,根据勾股定理求得OD,得出D的坐标,然后根据待定系数法即可求得反比例函数的解析式.
解答 解:在RT△OPD中,过P作PD⊥x轴于D,则PD=3,
∴OD=$\sqrt{O{P}^{2}-P{D}^{2}}$=4,
∴P(4,3),
∴代入反比例函数y=$\frac{k}{x}$得,3=$\frac{k}{4}$,
解得k=12,
∴反比例函数的解析式为y=$\frac{12}{x}$,
故选A.
点评 本题考查了待定系数法求反比例函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
15.抛物线y=ax2+bx+c(a<0)和直线y=mx+n(m≠0)相交于两点P(0,2)、Q(3,5),则不等式mx+n>ax2+bx+c的解集是( )
| A. | x<0 | B. | x>3 | C. | 0<x<3 | D. | x<0或x>3 |
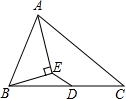 如图,AE平分∠BAC,BE⊥AE,垂足为E,D为BC的中点,∠BAE=36°,则∠BED的度数是126°.
如图,AE平分∠BAC,BE⊥AE,垂足为E,D为BC的中点,∠BAE=36°,则∠BED的度数是126°.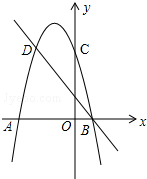 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.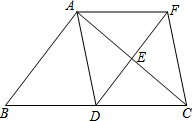 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.