题目内容
8.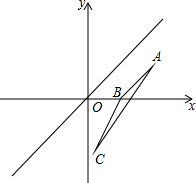 已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称.
已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称.(1)在所给的直角坐标系中作出△A1B1C1的图形;
(2)设点A的坐标是(4,2),求点A1的坐标;
(3)设BC所在的直线的解析式是y=2x-4,求B1C1边所在直线的解析式.
分析 (1)分别作A、B、C关于直线的对称点A1、B1、C1,依次连接各点,得到△A1B1C1即可;
(2)分别过点A、A1作坐标轴的垂线,证明构成的两个直角三角形全等,进而得出点A1坐标;
(3)在直线BC上选定两点(2,0)、(0,-4),由(2)得到,得出这两点关于直线l的对称点即可求出解析式.
解答  解:(1)分别作A、B、C关于直线的对称点A1、B1、C1,依次连接各点,得到△A1B1C1;
解:(1)分别作A、B、C关于直线的对称点A1、B1、C1,依次连接各点,得到△A1B1C1;
(2)分别过点A、A1作坐标轴的垂线A1M,AD,
∵直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称,
∴AB=A1B1,BO=OB1,MO=DO,
∴B1M=BD,
在Rt△A1MB1和Rt△ADB中
$\left\{\begin{array}{l}{{A}_{1}{B}_{1}=AB}\\{{B}_{1}M=BD}\end{array}\right.$,
∴Rt△A1MB1≌Rt△ADB(HL),
∵点A的坐标是(4,2),
∴点A1(2,4);
(3)在直线BC上选定两点(2,0)、(0,-4),由(2)得到,这两点关于直线l的对称点分别是(0,2)(-4,0),
设直线B1C1边所在直线的解析式为y=ax+b,
则$\left\{\begin{array}{l}{b=2}\\{-4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$.
所以B1C1边所在直线的解析式为:y=$\frac{1}{2}$x+2.
点评 此题主要考查了全等三角形的判定与性质以及待定系数法求一次函数解析式和轴对称变换,得出关于直线l的对称点位置是解题关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
19.在⊙O中,$\widehat{AB}$所对的圆心角为60°,半径为5cm,则$\widehat{AB}$的长为( )
| A. | $\frac{5}{3}$πcm | B. | $\frac{5}{6}$πcm | C. | $\frac{5\sqrt{3}}{3}$πcm | D. | $\frac{5\sqrt{3}}{6}$πcm |
13.函数y=$\sqrt{5+x}$中自变量x的取值范围是( )
| A. | x≥-5 | B. | x≥5 | C. | x>-5 | D. | x>5 |
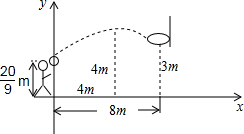 小明跳起投篮,已知球出手时离地面$\frac{20}{9}$m,球与篮筐中心的水平距离为8m,篮筐中心距地面3m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到高度4m,建立如图的平面直角坐标系.
小明跳起投篮,已知球出手时离地面$\frac{20}{9}$m,球与篮筐中心的水平距离为8m,篮筐中心距地面3m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到高度4m,建立如图的平面直角坐标系. 如图,MA,MB分别为⊙O的切线,A,B分别为切点,∠AMB=60°,点M到圆心O的距离OM=2,则⊙O的半径为1.
如图,MA,MB分别为⊙O的切线,A,B分别为切点,∠AMB=60°,点M到圆心O的距离OM=2,则⊙O的半径为1.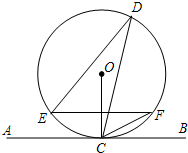 如图,直线AB切⊙O于点C,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于点H,连接CF,且CF=2,则EF的长为2$\sqrt{3}$.
如图,直线AB切⊙O于点C,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于点H,连接CF,且CF=2,则EF的长为2$\sqrt{3}$.