题目内容
16. 如图,MA,MB分别为⊙O的切线,A,B分别为切点,∠AMB=60°,点M到圆心O的距离OM=2,则⊙O的半径为1.
如图,MA,MB分别为⊙O的切线,A,B分别为切点,∠AMB=60°,点M到圆心O的距离OM=2,则⊙O的半径为1.
分析 根据切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角,可知∠APO的度数,连接OA,可知OA⊥AP,故在Rt△AOP中,根据三角函数公式,可将半径求出.
解答  解:连接OA.
解:连接OA.
∵PA为⊙O的切线,
∴PA⊥OA,
∵∠APO=$\frac{1}{2}$∠APB=30°,
∴OA=OP×sin∠APO=2×$\frac{1}{2}$=1,
∴⊙O的半径为1.
故答案为1.
点评 本题考查了切线的性质、直角三角函数以及圆的切线长定理,连接圆心和切点构建直角三角形是常用的辅助线的做法.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
7.已知(1-m2-n2)(m2+n2)=-6,则m2+n2的值是( )
| A. | 3 | B. | 3或-2 | C. | 2或-3 | D. | 2 |
11.泰州和姜堰某厂同时生产有某种型号的机器若干台,泰州厂可支援外地10台,姜堰厂可支援外地4台,兴化需要该种型号机器8台,泰兴需要6台,每台机器的运费(单位:元)如下表,设泰州运往兴化的机器为x台.
(1)用x的代数式表示:
(2)泰州运往兴化的运费是400x元
(3)若运这批机器的总运费为6800元,则泰州运往兴化的机器应为多少台?
| 终点 起点 | 泰兴 | 兴化 |
| 姜堰厂 | 300 | 500 |
| 泰州厂 | 600 | 400 |
| 终点 起点 | 泰兴 | 兴化 |
| 姜堰厂 | x-4 | 8-x |
| 泰州厂 | 10-x | x |
(3)若运这批机器的总运费为6800元,则泰州运往兴化的机器应为多少台?
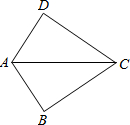 如图,已知AC是∠BAD的平分线,请添加一个条件使△ABC≌△ADC,则需添加的条件是AD=AB(只需写一个正确答案).
如图,已知AC是∠BAD的平分线,请添加一个条件使△ABC≌△ADC,则需添加的条件是AD=AB(只需写一个正确答案). 如图,AD⊥BC于点D,BD=DC,点C在AE的垂直平分线上,DE=8,则AB+BD=8.
如图,AD⊥BC于点D,BD=DC,点C在AE的垂直平分线上,DE=8,则AB+BD=8.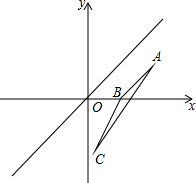 已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称.
已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称.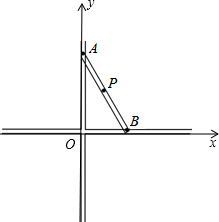 著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能分别在纵向滑槽内、横向滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.按如图所示建立平面直角坐标系.已知AB=10cm,
著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能分别在纵向滑槽内、横向滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.按如图所示建立平面直角坐标系.已知AB=10cm,