题目内容
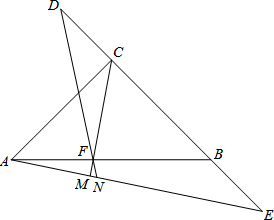 如图,在等腰三角形ABC中,CA=CB,∠ACB=90°,点D、E是直线BC上两点且CD=BE,过点C作CM⊥AE交AE于点M,交AB于点F,连接DF并延长交AE于点N.
如图,在等腰三角形ABC中,CA=CB,∠ACB=90°,点D、E是直线BC上两点且CD=BE,过点C作CM⊥AE交AE于点M,交AB于点F,连接DF并延长交AE于点N.(1)若AC=2,CD=1,求CM的值;
(2)求证:∠D=∠E.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据题意可求AC,CE,根据勾股定理可得AB的长,再根据三角形的面积公式即可得到CM的值;
(2)过点B作BH⊥CB交CM的延长线于点H.通过ASA证明△ACE≌△CBH,得到∠E=∠H,通过SAS证明△DBF≌△HBF,得到∠D=∠H,依此即可求解.
(2)过点B作BH⊥CB交CM的延长线于点H.通过ASA证明△ACE≌△CBH,得到∠E=∠H,通过SAS证明△DBF≌△HBF,得到∠D=∠H,依此即可求解.
解答:解:(1)∵CD=BE,CD=1,
∴BE=1,
又∵AC=CB=2,
∴CE=CB+BE=3,
在Rt△AEC中,AE=
=
,
∴CM=
=
;
 (2)过点B作BH⊥CB交CM的延长线于点H.
(2)过点B作BH⊥CB交CM的延长线于点H.
∴∠HBC=∠CMA=90°,
∴∠CAM+∠ACM=90°,
∴∠ACM+∠ECM=90°
∴∠CAM=∠ECM,
又∵BH⊥CB,
∴∠CBH=90°,
在△ACE和△CBH中,
,
∴△ACE≌△CBH(ASA),
∴CE=BH,∠E=∠H,
又∵△ABC为等腰直角三角形,
∴∠CBF=45°,
又∵∠CBH=90°,
∴∠FBH=45°,
∴∠FBH=∠CBF,
在△DBF和△HBF中,
,
∴△DBF≌△HBF(SAS),
∴∠D=∠H=∠E.
∴BE=1,
又∵AC=CB=2,
∴CE=CB+BE=3,
在Rt△AEC中,AE=
| 22+32 |
| 13 |
∴CM=
| 6 | ||
|
6
| ||
| 13 |
 (2)过点B作BH⊥CB交CM的延长线于点H.
(2)过点B作BH⊥CB交CM的延长线于点H.∴∠HBC=∠CMA=90°,
∴∠CAM+∠ACM=90°,
∴∠ACM+∠ECM=90°
∴∠CAM=∠ECM,
又∵BH⊥CB,
∴∠CBH=90°,
在△ACE和△CBH中,
|
∴△ACE≌△CBH(ASA),
∴CE=BH,∠E=∠H,
又∵△ABC为等腰直角三角形,
∴∠CBF=45°,
又∵∠CBH=90°,
∴∠FBH=45°,
∴∠FBH=∠CBF,
在△DBF和△HBF中,
|
∴△DBF≌△HBF(SAS),
∴∠D=∠H=∠E.
点评:考查了全等三角形的判定与性质,勾股定理,三角形的面积计算,以及等腰直角三角形的性质,综合性较强,有一定的难度.

练习册系列答案
相关题目
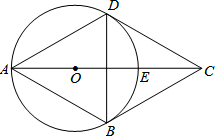 已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.
已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.
 如图,在△ABC中,AB=2,BC=3.5,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
如图,在△ABC中,AB=2,BC=3.5,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为