题目内容
在圆O中，弦AB为圆内接正六边形的边长，弦AC为圆内接正方形的边长，那么∠BAC= ．
考点：正多边形和圆
专题：
分析：
如图，根据正多边形和圆得出∠OAB=60°，∠OAC=45°，从而得出∠BAC的度数．
如图，根据正多边形和圆得出∠OAB=60°，∠OAC=45°，从而得出∠BAC的度数．解答：解：如图，
∵弦AB为圆内接正六边形的边长，弦AC为圆内接正方形的边长，
∴∠OAB=60°，∠OAC=45°，
∴∠BAC=∠OAB-∠OAC=60°-45°=15°，
故答案为15°．
解：如图，∵弦AB为圆内接正六边形的边长，弦AC为圆内接正方形的边长，
∴∠OAB=60°，∠OAC=45°，
∴∠BAC=∠OAB-∠OAC=60°-45°=15°，
故答案为15°．
点评：本题考查了正多边形和圆，计算正多边形的中心角是解题的关键．
练习册系列答案
相关题目
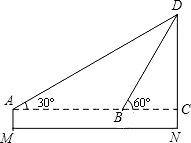在测量操场旗杆高度的综合实践活动中某小组测绘了如下所示的示意图其中测角仪的高为1.5m，在A处测得旗杆顶部D的倾角为30°，他把测角仪向前搬了10m到达B处后，在此测得旗杆顶部D的仰角为60°，求旗杆DN的高度（结果保留小数点后一位．）
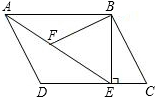如图，在平行四边形ABCD中，AB=4，BC=3，过点B作BE⊥CD于E，连接AE，∠AEB=60°，F为AE上一点，且∠BFE=∠C．