题目内容
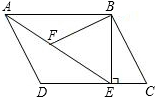 如图,在平行四边形ABCD中,AB=4,BC=3,过点B作BE⊥CD于E,连接AE,∠AEB=60°,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,AB=4,BC=3,过点B作BE⊥CD于E,连接AE,∠AEB=60°,F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD;
(2)求AE的长;
(3)求BF的长.
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:(1)可通过证明∠BAF=∠AED,∠AFB=∠D,证得△ABF∽△EAD;
(2)根据平行线的性质得出∠ABE=90°,进而利用锐角三角函数关系求出AE的长即可;
(3)利用△ABF∽△EAD,进而得出
=
,求出BF的长即可.
(2)根据平行线的性质得出∠ABE=90°,进而利用锐角三角函数关系求出AE的长即可;
(3)利用△ABF∽△EAD,进而得出
| BF |
| AD |
| AB |
| AE |
解答:(1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°,
∵∠AEB=60°,
∴tan60°=
=
,
故BE=
,
则AE=
;
(3)解:∵由(1)知,△ABF∽△EAD,
∴
=
∴
=
∴BF=
.
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°,
∵∠AEB=60°,
∴tan60°=
| AB |
| EB |
| 3 |
故BE=
4
| ||
| 3 |
则AE=
8
| ||
| 3 |
(3)解:∵由(1)知,△ABF∽△EAD,
∴
| BF |
| AD |
| AB |
| AE |
∴
| BF |
| 3 |
| 4 | ||||
|
∴BF=
3
| ||
| 2 |
点评:本题主要考查了三角形的判定和性质以及平行四边形的性质等知识点,得出△ABF∽△EAD是解题关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
下列表述准确规范的是( )
| A、延长直线AB到C |
| B、延长射线AB(A是端点)到C |
| C、延长线段AB到C,使BC=AB |
| D、直线a、b相交于m |
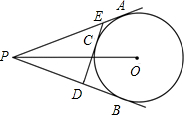 如图,PA、PB、DE分别切⊙O于点A、B、C,⊙O的半径为6,OP=10.求△PDE的周长.
如图,PA、PB、DE分别切⊙O于点A、B、C,⊙O的半径为6,OP=10.求△PDE的周长.