题目内容
七中育才学校为鼓励学生进行微电影拍摄,出台了相关规定:由学校统一给学生提供光碟刻录,学生在教育研讨会期间自主销售,刻录成本价与出厂价之间的差价由学校承担.李明按照规定拍摄了一部质量较高的微电影.已知该部微电影光盘的成本价为每盘10元,刻录商家出厂价为每盘12元,销售量y(盘)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明把销售单价定为20元,那么学校为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,可获得最大利润?
(3)学校规定销售单价不得高于25元.如果李明想要获得的利润不低于3000元,那么学校为他承担的总差价最少为多少元?
(1)李明把销售单价定为20元,那么学校为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,可获得最大利润?
(3)学校规定销售单价不得高于25元.如果李明想要获得的利润不低于3000元,那么学校为他承担的总差价最少为多少元?
考点:二次函数的应用
专题:
分析:(1)把x=20代入y=-10x+500求出销售的件数,然后求出学校承担的成本价与出厂价之间的差价;
(2)由利润=销售价-成本价,得w=(x-10)(-10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;
(3)令-10x2+600x-5000=3000,求出x的值,结合图象求出利润的范围,然后设设学校每个月为他承担的总差价为p元,根据一次函数的性质求出总差价的最小值.
(2)由利润=销售价-成本价,得w=(x-10)(-10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;
(3)令-10x2+600x-5000=3000,求出x的值,结合图象求出利润的范围,然后设设学校每个月为他承担的总差价为p元,根据一次函数的性质求出总差价的最小值.
解答:解:(1)当x=20时,y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600元,
即学校这个月为他承担的总差价为600元.
(2)依题意得,w=(x-10)(-10x+500)
=-10x2+600x-5000
=-10(x-30)2+4000
∵a=-10<0,∴当x=30时,w有最大值4000元.
即当销售单价定为30元时,每月可获得最大利润4000元.
(3)由题意得:-10x2+600x-5000=3000,
解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,
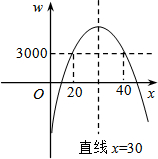
∴结合图象可知:当20≤x≤40时,4000>w≥3000.
又∵x≤25,
∴当20≤x≤25时,w≥3000.
设学校每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500元.
即销售单价定为25元时,学校每个月为他承担的总差价最少为500元.
300×(12-10)=300×2=600元,
即学校这个月为他承担的总差价为600元.
(2)依题意得,w=(x-10)(-10x+500)
=-10x2+600x-5000
=-10(x-30)2+4000
∵a=-10<0,∴当x=30时,w有最大值4000元.
即当销售单价定为30元时,每月可获得最大利润4000元.
(3)由题意得:-10x2+600x-5000=3000,
解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,

∴结合图象可知:当20≤x≤40时,4000>w≥3000.
又∵x≤25,
∴当20≤x≤25时,w≥3000.
设学校每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500元.
即销售单价定为25元时,学校每个月为他承担的总差价最少为500元.
点评:本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解,此题难度不大.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 某城市12个月平均最高气温T(℃)与月份m的函数关系如图,求该城市1月,7月的平均最高气温.
某城市12个月平均最高气温T(℃)与月份m的函数关系如图,求该城市1月,7月的平均最高气温. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为F,点E在⊙O上,∠ABD与∠AEC相等吗?为什么?
如图,AB是⊙O的直径,弦CD⊥AB,垂足为F,点E在⊙O上,∠ABD与∠AEC相等吗?为什么?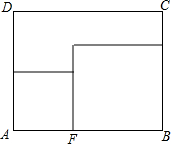 如图,矩形纸片ABCD,AD=8,AB=10,点F在AB上,分别以AF、FB为边裁出的两个小正方形纸片面积和S的取值范围是
如图,矩形纸片ABCD,AD=8,AB=10,点F在AB上,分别以AF、FB为边裁出的两个小正方形纸片面积和S的取值范围是