题目内容
5.解方程:(1)36(-x+1)2=25
(2)2(x-1)3=-$\frac{125}{4}$.
分析 (1)用直接开平方解方程即可,
(2)用直接开立方解高次方程即可.
解答 解:(1)∵36(-x+1)2=25,
∴(-x+1)2=$\frac{25}{36}$,
∴-x+1=±$\frac{5}{6}$,
∴x1=$\frac{1}{6}$,x2=$\frac{11}{6}$.
(2)∵2(x-1)3=-$\frac{125}{4}$,
∴(x-1)3=-$\frac{125}{8}$,
∴x-1=-$\frac{5}{2}$,
∴x=-$\frac{3}{2}$.
点评 此题是立方根题,主要考查了立方根,平方根的意义解二次,三次方程,解本题的关键是熟练掌握立方根,平方根的意义.

练习册系列答案
相关题目
17.超市为减小A商品的积压,决定采取降价销售的策略,若某商品的原价为52元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
(1)这个表反映了降价和日销量两个变量之间的关系;
(2)从表中可以看出每降价1元,日销量增加5件;
(3)可以估计降价之前的日销量为150件;
(4)设日销量为y件,降价为x元,则y与x的函数关系式为y=5x+150;
(5)当售价为44元时,日销量为190件.
| 降价(元) | 1 | 2 | 3 | 4 | 5 | 6 |
| 日销量(件) | 155 | 160 | 165 | 170 | 175 | 180 |
(2)从表中可以看出每降价1元,日销量增加5件;
(3)可以估计降价之前的日销量为150件;
(4)设日销量为y件,降价为x元,则y与x的函数关系式为y=5x+150;
(5)当售价为44元时,日销量为190件.
 某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: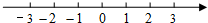
 小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.