题目内容
9.已知α为锐角,则sinα的值不可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
分析 根据α是锐角,判断出sinα的取值范围,即可判断出sinα的值不可能为选项中的哪个数.
解答 解:∵α是锐角,
∴sinα的取值范围是:0<sinα<1,
∴sinα的值不可能为2.
故选:D.
点评 此题主要考查了正弦函数的定义:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.即sinA=∠A的对边:斜边=a:c.定义要熟练掌握,解答此题的关键是根据α是锐角,判断出sinα的取值范围.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
4. 如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )
如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )
 如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )
如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )| A. | 60° | B. | 90° | C. | 105° | D. | 120° |
1.下列各数中,没有平方根的是( )
| A. | 4 | B. | 0 | C. | $\frac{1}{8}$ | D. | -9 |
18.若一个三角形成轴对称图形,且有一个内角为60°,则这个三角形一定是( )
| A. | 直角三角形 | B. | 等腰直角三角形 | ||
| C. | 等边三角形 | D. | 底和腰不相等的等腰三角形 |
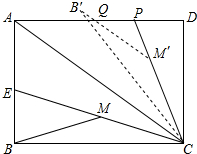 已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$. 已知二次函数y=x2+bx+c的图象经过点(1,0)、(4,3).
已知二次函数y=x2+bx+c的图象经过点(1,0)、(4,3). 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).