题目内容
19.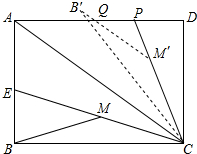 已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
分析 首先证明四边形ACM'Q是等腰梯形,设PQ=x,在直角△CDP中,根据勾股定理即可得到关于x的方程求得x的值.
解答 解:设PQ=x,
∵CE平分∠ACB,
∴∠BCE=∠ACE,且$\frac{BE}{AE}$=$\frac{BC}{AC}$,
∵AB=3,BC=4,
∴AC=5,
∴$\frac{BE}{AE}=\frac{4}{5}$,
∴BE=$\frac{4}{3}$,AE=$\frac{5}{3}$,
∴CE=$\frac{4\sqrt{10}}{3}$,
∴CM=$\frac{2\sqrt{10}}{3}$.
∵M是CE的中点,且△BCE是直角三角形,
∴BM=CM=EM,
∴∠CBM=∠BCM=∠ACE,
又△B'CM'是△BCM旋转得到,
∴△B'CM'≌△BCM.
∵PQ=P'M,
∴∠PM'Q=∠PQM'=2∠B'CM'=∠ACB.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ACB=∠CAD,
∴∠PQM'=CAD,
∴AC∥B'M',
∴∠PM'Q=∠ACP,
∴∠CAD=∠ACP,
∴四边形ACM'Q是等腰梯形,
∴AQ=CM'=$\frac{2\sqrt{10}}{3}$,
∴PD=$\frac{2\sqrt{10}}{3}$+x,
在直角△CDP中,根据勾股定理得:CP2=PD2+CD2,
($\frac{2\sqrt{10}}{3}$+x)2=(4-$\frac{2\sqrt{10}}{3}$-x)2+9,另t=$\frac{2\sqrt{10}}{3}$+x,则t2=(4-t)2+9,
∴t=$\frac{25}{8}$,
∴$\frac{2\sqrt{10}}{3}$+x=$\frac{25}{8}$,
∴x=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$,
∴PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
故答案是:$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
点评 本题考查了图形的旋转,以及等腰梯形的证明和勾股定理的应用,证明四边形ACM'Q是等腰梯形是本题的关键.

| A. | 1 | B. | -1 | C. | 1或-1 | D. | $\frac{1}{2}$ |
| A. | -2 | B. | 3 | C. | -3 | D. | 2 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
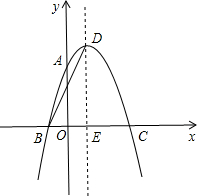 如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题: 如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.
如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.