题目内容
17.计算:(1)-11+22-(-33)
(2)(-$\frac{1}{2}+\frac{2}{3}-\frac{1}{9}$)÷(-$\frac{1}{18}$)
(3)36÷[(-3)2-(-3)]
(4)-3×$(-\frac{1}{2})^{3}-(\frac{1}{3})^{2}÷(-\frac{2}{3})^{2}$.
分析 (1)首先化简,然后正数先相加,然后加上负数即可;
(2)首先转化为乘法运算,然后利用分配律计算即可;
(3)首先计算乘方,计算括号内的式子,然后进行除法计算;
(4)首先计算乘方,然后进行乘除计算,最后进行加减即可.
解答 解:(1)原式=-11+22+33=-11+33=44;
(2)原式=(-$\frac{1}{2}+\frac{2}{3}-\frac{1}{9}$)×(-18)=$\frac{1}{2}$×18-$\frac{2}{3}$×18+$\frac{1}{9}$×18=9-12+2=-1;
(3)原式=36÷【9+3】=36÷12=3;
(4)原式=-3×(-$\frac{1}{8}$)-$\frac{1}{9}$÷$\frac{4}{9}$=$\frac{3}{8}$-$\frac{1}{9}$×$\frac{9}{4}$=$\frac{3}{8}$-$\frac{1}{4}$=$\frac{1}{8}$.
点评 本题考查的是有理数的运算与整式的加减运算.注意:要正确掌握运算顺序,即乘方运算(和以后学习的开方运算)叫做三级运算;乘法和除法叫做二级运算;加法和减法叫做一级运算.在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.关于x的一元二次方程x2+3x-2=0两根之积等于( )
| A. | -2 | B. | 3 | C. | -3 | D. | 2 |
5.在数轴上表示下列各数,其中与表示-$\frac{1}{2}$的点位置最近的数是( )
| A. | -2 | B. | 0 | C. | 2 | D. | -3 |
2.小明根据柸州市出租车的收费标准,制定了打车费计算的数值转换机示意图:

(1)根据数值转换机程序计算下列乘客应付打车费用:
(2)通过填写表格,用一句话描述你的发现:当乘车的里程大于2公里时,乘车费用随着乘车的里程增大而增大
(3)请用代数式表示上述数值转换程序.

(1)根据数值转换机程序计算下列乘客应付打车费用:
| 乘客 | 甲 | 乙 | 丙 | 丁 | 戍 |
| 输入/公里 | 1.5 | 2 | 4 | 6 | 8 |
| 输出/元 | 5 | 5 | 8 | 11 | 14 |
(3)请用代数式表示上述数值转换程序.
9.已知α为锐角,则sinα的值不可能为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
7. 有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )
有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )
 有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )
有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )| A. | -a>b | B. | -a=b | C. | -a<b | D. | 不能判断 |
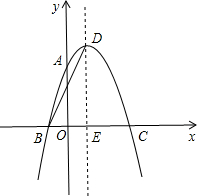 如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题: 如图,南北向的公路上有一点A,东西向的公路上有一点B,若要在两条公路上确定点P,使得△PAB是等腰三角形,则这样的点P最多能确定8个.
如图,南北向的公路上有一点A,东西向的公路上有一点B,若要在两条公路上确定点P,使得△PAB是等腰三角形,则这样的点P最多能确定8个.