题目内容
 已知,如图所示,△ABC中,∠ACB=60°,延长AC到D,使CD=
已知,如图所示,△ABC中,∠ACB=60°,延长AC到D,使CD=| 1 |
| 2 |
考点:解直角三角形
专题:计算题
分析:作AE⊥BC于E,连接DE,如图,设CD=a,则AC=2a,在Rt△AEC中,由于∠ACB=60°,根据含30度的直角三角形三边的关系得CE=
AC=a,则CE=CD,根据等腰三角形的性质得∠CED=∠CDE,再根据三角形外角性质可计算出∠CDE=30°,于是有∠EAD=∠EDA=30°,则ED=EA;接着计算∠EDB=∠CDB=15°,∠CBD=15°,由此得到EB=ED,所以AE=BE,于是可得到∠ABC=45°.
| 1 |
| 2 |
解答:解:作AE⊥BC于E,连接DE,如图,设CD=a, 则AC=2a,
则AC=2a,
在Rt△AEC中,∵∠ACB=60°,
∴∠EAC=30°,
∴CE=
AC=a,
∴CE=CD,
∴∠CED=∠CDE,
而∠CED+∠CDE=∠ACE=60°,
∴∠CDE=30°,
∴∠EAD=∠EDA=30°,
∴ED=EA,
∵∠CDB=45°,
∴∠EDB=∠CDB=15°,
∵∠ACB=∠CBB+∠CBD,
∴∠CBD=60°-45°=15°,
∴∠EBD=∠EDB,
∴EB=ED,
∴AE=BE,
∴△ABE为等腰直角三角形,
∴∠ABC=45°.
 则AC=2a,
则AC=2a,在Rt△AEC中,∵∠ACB=60°,
∴∠EAC=30°,
∴CE=
| 1 |
| 2 |
∴CE=CD,
∴∠CED=∠CDE,
而∠CED+∠CDE=∠ACE=60°,
∴∠CDE=30°,
∴∠EAD=∠EDA=30°,
∴ED=EA,
∵∠CDB=45°,
∴∠EDB=∠CDB=15°,
∵∠ACB=∠CBB+∠CBD,
∴∠CBD=60°-45°=15°,
∴∠EBD=∠EDB,
∴EB=ED,
∴AE=BE,
∴△ABE为等腰直角三角形,
∴∠ABC=45°.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.记住含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
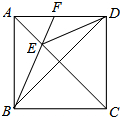 如图,在正方形ABCD中,E为对角线AC上一点,连结EB,ED,BD,延长BE交AD于点F,DF2=EF•BF.
如图,在正方形ABCD中,E为对角线AC上一点,连结EB,ED,BD,延长BE交AD于点F,DF2=EF•BF.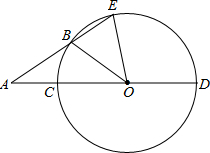 如图,CD是⊙O的直径,A为OC延长线上一点,E为⊙O上一点,AE交⊙O于点B.若点B是
如图,CD是⊙O的直径,A为OC延长线上一点,E为⊙O上一点,AE交⊙O于点B.若点B是
 如图所示,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.
如图所示,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切. 如图为一个长4cm,宽2cm,高1cm的实心长方体,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对面顶点G处,问怎样走路线最短?最短路线长为多少?
如图为一个长4cm,宽2cm,高1cm的实心长方体,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对面顶点G处,问怎样走路线最短?最短路线长为多少? 如图,四边形ABCD中,AD∥BC,AC平分∠BAD,BD平分∠ABC,试判断四边形ABCD的形状并证明.
如图,四边形ABCD中,AD∥BC,AC平分∠BAD,BD平分∠ABC,试判断四边形ABCD的形状并证明. 如图,A、B是直线l同侧的两定点,定长线段PQ在l上移动,问P、Q移动到什么地方AP+PQ+QB的长最短?
如图,A、B是直线l同侧的两定点,定长线段PQ在l上移动,问P、Q移动到什么地方AP+PQ+QB的长最短?