题目内容
如图，A、B是直线l同侧的两定点，定长线段PQ在l上移动，问P、Q移动到什么地方AP+PQ+QB的长最短？考点：轴对称-最短路线问题
专题：
分析：作A点关于直线l的对称点A′，过B点作直线l的平行线m，在平行线m上截取BB′=PQ，连接A′B′，交直线l于P点，即可求得P、Q的位置．
解答：解：如图所示，
作A点关于直线l的对称点A′，过B点作直线l的平行线m，在平行线m上截取BB′=PQ，连接A′B′，交直线l于P点，此时AP+PQ+QB的长最短．
作A点关于直线l的对称点A′，过B点作直线l的平行线m，在平行线m上截取BB′=PQ，连接A′B′，交直线l于P点，此时AP+PQ+QB的长最短．
点评：本题考查了利用轴对称求解最短路径的问题，注意仔细理解，灵活运用题目所给的信息，规范作图．
练习册系列答案
名校课堂系列答案
相关题目
已知，如图所示，△ABC中，∠ACB=60°，延长AC到D，使CD=对于正整数x，现定义f（x）=
，则有f（1）=
，f（2）=
，f（3）=
，…，试求：f（1）+f（2）+f（3）+…+f（n-1）+f（n）的值（其中n为正整数）．
| 2 |
| x(x+2) |
| 2 |
| 1×3 |
| 2 |
| 2×4 |
| 2 |
| 3×5 |
已知△ABC在平面直角坐标系中的位置如图所示，则在△ABC关于直线l对称的图形中，点A的对应点的坐标为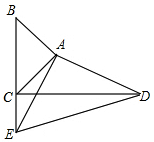
如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，点B、C、E在同一条直线上，AC=AB，AD=AE．求证：
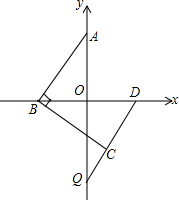已知如图在平面直角坐标系中，点A（0，m），点D（n，0），若|m-a|+（n-b）2=0，a=b．在x轴的负半轴上有一动点B，连接AB，过点B作BC⊥AB，且BC=AB，连接DC并延长交y轴于点Q，试问当B点运动时，点Q的位置是否发生变化？请先作出判断，然后证明你的结论．
将1、下列代数式是一次式的是（ ）
| A、8 | ||
| B、4s+3t | ||
C、
| ||
D、
|