题目内容
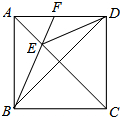 如图,在正方形ABCD中,E为对角线AC上一点,连结EB,ED,BD,延长BE交AD于点F,DF2=EF•BF.
如图,在正方形ABCD中,E为对角线AC上一点,连结EB,ED,BD,延长BE交AD于点F,DF2=EF•BF.(1)求证:DE平分∠ADB;
(2)求tan∠BEC的值.
考点:正方形的性质,相似三角形的判定与性质
专题:
分析:(1)由条件可得△FED∽△FDB,可证得∠FDE=∠FBD,又由正方形的对称性可得BE=DE,可得∠EBD=∠EDB,可得出结论;
(2)设对角线AC和BD交于点O,在Rt△EBO中可表示出tan∠BEC,再利用角平分线的性质得到AE和EO的比例关系,从而求出EO和BO的比,得出结论.
(2)设对角线AC和BD交于点O,在Rt△EBO中可表示出tan∠BEC,再利用角平分线的性质得到AE和EO的比例关系,从而求出EO和BO的比,得出结论.
解答:(1)证明:∵DF2=EF.BF,
∴DF:BF=EF:DF,∠EFD=∠BFD,
∴△FED∽△FDB,
∴∠FDE=∠FBD,
又∵E在对角线AC上,由正方形的对称性可得EB=ED,
∴∠EBD=∠EDB,
∴∠FDE=∠EDB,
∴DE平分∠ADB;
 (2)解:设AC、BD交于点O,
(2)解:设AC、BD交于点O,
∵DE平分∠ADB,
∴
=
=
,
∴
=
=
-1,
即
=
-1,
在Rt△BOE中,tan∠BEC=
=
=
-1.
∴DF:BF=EF:DF,∠EFD=∠BFD,
∴△FED∽△FDB,
∴∠FDE=∠FBD,
又∵E在对角线AC上,由正方形的对称性可得EB=ED,
∴∠EBD=∠EDB,
∴∠FDE=∠EDB,
∴DE平分∠ADB;
 (2)解:设AC、BD交于点O,
(2)解:设AC、BD交于点O,∵DE平分∠ADB,
∴
| EO |
| AE |
| OD |
| AD |
| 1 | ||
|
∴
| EO |
| AE+EO |
| 1 | ||
1+
|
| 2 |
即
| EO |
| AO |
| 2 |
在Rt△BOE中,tan∠BEC=
| EO |
| BO |
| EO |
| AO |
| 2 |
点评:本题主要考查正方形的性质及相似三角形的判定和性质,在(1)中注意正方形对称性的运用,在(2)中利用角平分线的性质是解题的关键.

练习册系列答案
相关题目
 如图,AB∥CD,若∠C=75°,则∠AEF=
如图,AB∥CD,若∠C=75°,则∠AEF= 已知,如图所示,△ABC中,∠ACB=60°,延长AC到D,使CD=
已知,如图所示,△ABC中,∠ACB=60°,延长AC到D,使CD=