题目内容
 如图所示,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.
如图所示,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.考点:切线的判定
专题:证明题
分析:利用圆周角定理进而得出∠EBA=90°,再利用角平分线的性质以及外角的性质和等腰三角形的性质求出∠1=∠ABC,以及∠CAE+∠1=90°,进而得出答案.
解答: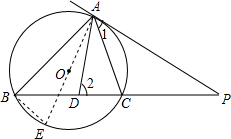 解:连接AO并延长交⊙O于点E,连接BE,
解:连接AO并延长交⊙O于点E,连接BE,
∵AE为⊙O的直径,
∴∠EBA=90°,
∵PA=PD,
∴∠1+∠CAD=∠2,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠ABD+∠BAD=∠2,
∴∠1=∠ABC,
∵∠CBE=∠EAC,∠ABC+∠CBE=90°,
∴∠CAE+∠1=90°,
∴PA与⊙O相切.
 解:连接AO并延长交⊙O于点E,连接BE,
解:连接AO并延长交⊙O于点E,连接BE,∵AE为⊙O的直径,
∴∠EBA=90°,
∵PA=PD,
∴∠1+∠CAD=∠2,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠ABD+∠BAD=∠2,
∴∠1=∠ABC,
∵∠CBE=∠EAC,∠ABC+∠CBE=90°,
∴∠CAE+∠1=90°,
∴PA与⊙O相切.
点评:此题主要考查了切线的判定以及圆周角定理以及三角形外角的性质和等腰三角形的性质等知识,得出∠1=∠ABC是解题关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
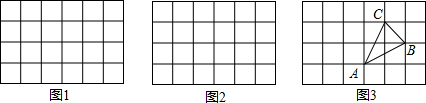
 已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系.
已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系. 已知,如图所示,△ABC中,∠ACB=60°,延长AC到D,使CD=
已知,如图所示,△ABC中,∠ACB=60°,延长AC到D,使CD= 如图,已知点A的坐标为(-16,0),过点A的直线交y轴于点C,OB⊥AC于点B,
如图,已知点A的坐标为(-16,0),过点A的直线交y轴于点C,OB⊥AC于点B,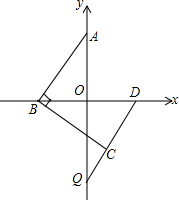 已知如图在平面直角坐标系中,点A(0,m),点D(n,0),若|m-a|+(n-b)2=0,a=b.在x轴的负半轴上有一动点B,连接AB,过点B作BC⊥AB,且BC=AB,连接DC并延长交y轴于点Q,试问当B点运动时,点Q的位置是否发生变化?请先作出判断,然后证明你的结论.
已知如图在平面直角坐标系中,点A(0,m),点D(n,0),若|m-a|+(n-b)2=0,a=b.在x轴的负半轴上有一动点B,连接AB,过点B作BC⊥AB,且BC=AB,连接DC并延长交y轴于点Q,试问当B点运动时,点Q的位置是否发生变化?请先作出判断,然后证明你的结论.