题目内容
4．
如图，在△ABC中，D、E分别是AB和AC上的点，DE∥BC，AD=3BD，S△ABC=48，求S△ADE的值．
分析 根据DE∥BC，可以得出△ADE∽△ABC；根据相似三角形面积的比等于相似比的平方，求出了相似比就可以求出△ADE的面积．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=${（\frac{AD}{AB}）}^{2}$，
∵AD=3BD，
∴$\frac{AD}{AB}$=$\frac{3}{4}$，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=${（\frac{AD}{AB}）}^{2}$=$\frac{9}{16}$，
∵S△ABC=48，
∴S△ADE=27．
点评 本题考查了相似三角形性质和判定，相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
13．若关于y的一元二次方程ky2-7y-7=0有实根，则k的取值范围是（ ）
| A． | k＞-$\frac{7}{4}$ | B． | k≥-$\frac{7}{4}$且k≠0 | C． | k≤-$\frac{7}{4}$ | D． | k＞-$\frac{7}{4}$且k≠0 |
14．
已知二次函数y=ax2+bx+c（a≠0）的图象如图，分析下列四个结论：
①abc＜0；②b2-4ac＞0；③3a+c＞0；④（a+c）2＜b2，其中正确的结论为（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2-4ac＞0；③3a+c＞0；④（a+c）2＜b2，其中正确的结论为（ ）
| A． | ①② | B． | ②④ | C． | ①③④ | D． | ①③ |
11．将直角坐标系中的点（-1，-3）向上平移4个单位，再向右平移2个单位后的点的坐标为（ ）
| A． | （3，-1） | B． | （-5，-1） | C． | （-3，1） | D． | （1，1） |
如图，DE是△ABC的中位线，则△ADE与四边形DBCE的面积之比是1：3．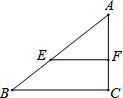
如图Rt△ABC中，∠C=90°，E为AB边上一点，F为AC边上一点，EF∥BC，AE=5，AF=BE=3，则BC=$\frac{32}{8}$．
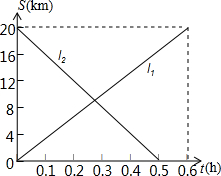甲、乙两辆摩托车分别从A、B两地同时出发相向而行，两辆摩托车与A地的距离S（km）与行驶时间t（min）之间的函数关系如图，则下列说法中正确的有（ ）