题目内容
12.已知二次函数y=2x2-4x-6.(1)用配方法将y=2x2-4x-6化成y=a(x-h)2+k的形式;
(2)在所给的平面直角坐标系中,画出这个二次函数的图象;
(3)当x取何值时,y随x的增大而减少?
(4)当x取何值是,y<0?
分析 (1)利用配方法易得y=2(x-1)2-8,则抛物线的顶点坐标为(1,-8),对称轴为直线x=1;
(2)利用描点法画二次函数图象;
(3)根据二次函数的性质求解;
(4)观察函数图象,找出图象在x轴下方所对应的自变量的取值范围.
解答  解:(1)y=2(x2-2x)-6
解:(1)y=2(x2-2x)-6
=2(x2-2x+1-1)-6
=2(x-1)2-8;
(2)如图:
(3)当x<1时,y随x的增大而减少;
(4)当-1<x<3时,y<0.
点评 本题考查了二次函数的三种形式:一般式:y=ax2+bx+c(a,b,c是常数,a≠0);顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(h,k);交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0),该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标(x1,0),(x2,0).也考查了二次函数图象与性质.

练习册系列答案
相关题目
2. 如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )
如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )
 如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )
如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
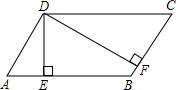 如图,平行四边形ABCD中,∠C=60°,DE⊥AB于E,DF⊥BC于F,则∠EDF=60°.
如图,平行四边形ABCD中,∠C=60°,DE⊥AB于E,DF⊥BC于F,则∠EDF=60°.