题目内容
17．正方形ABCD中，AB=2，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是$\sqrt{5}$．分析 由于点B与点D关于AC对称，所以如果连接DE，交AC于点P，那PE+PB的值最小．在Rt△CDE中，由勾股定理先计算出DE的长度，即为PE+PB的最小值．
解答 
解：连接DE，交AC于点P，连接BD．
∵点B与点D关于AC对称，
∴DE的长即为PE+PB的最小值，
∵AB=2，E是BC的中点，
∴CE=1，
在Rt△CDE中，
DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$．
故答案为：$\sqrt{5}$．
点评 本题考查了轴对称-最短路线问题和正方形的性质，根据两点之间线段最短，可确定点P的位置．
练习册系列答案
阅读快车系列答案
相关题目
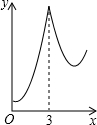
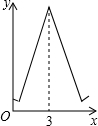
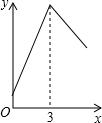
如图，正△ABC的边长为3，点N在AC边上且AN：NC=1：2，三角形边上的动点M从点A出发，沿A→B→C的方向运动，到达点C时停止．设点M运动的路程为x，y=MN2，则y关于x的函数图象大致为（ ）
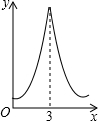
如图，已知直线l1：y=-x+5，直线l2：y=2x+2，两直线交于点A，l1交x轴于C点，l2交y轴于点B，交x轴于点D．