题目内容
4.命题“线段的中点到这条线段两端的距离相等”的逆命题是到线段两端的距离相等的点是这条线段的中点.分析 交换原命题的题设与结论部分即可得到原命题的逆命题.
解答 解:命题“线段的中点到这条线段两端的距离相等”的逆命题是到线段两端的距离相等的点是这条线段的中点.
故答案为到线段两端的距离相等的点是这条线段的中点.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
19. 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 1.4 |
13.某公司的仓库中原先有1.5万件货物,后又运出0.7万件,过了一段时间后计划往仓库中补充1.2万件,但因为某些原因,少往仓库中补充0.3万件,则现在仓库中的货物有( )
| A. | 1.8万件 | B. | 1.7万件 | C. | 1.5万件 | D. | 1.1万件 |
14.下列运算中,正确的是( )
| A. | $\sqrt{3+4}$=$\sqrt{3}$+$\sqrt{4}$ | B. | $\sqrt{4-3}$=$\sqrt{4}$-$\sqrt{3}$ | C. | $\sqrt{{4}^{2}-{3}^{2}}$=4-3 | D. | $\sqrt{(4+3)^{2}}$=4+3 |
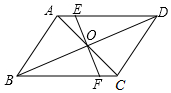 如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.