题目内容
7.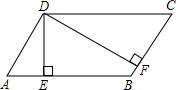 如图,平行四边形ABCD中,∠C=60°,DE⊥AB于E,DF⊥BC于F,则∠EDF=60°.
如图,平行四边形ABCD中,∠C=60°,DE⊥AB于E,DF⊥BC于F,则∠EDF=60°.
分析 由平行四边形的性质得出∠A=∠C=60°,∠B=180°-∠A=120°,再由四边形内角和定理即可得出∠EDF的度数.
解答 解:∵四边形ABCD是平行四边形,
∴∠A=∠C=60°,
∴∠B=180°-∠A=120°,
∵DE⊥AB于E,DF⊥BC于F,
∴∠DEB=∠DFB=90°,
∴∠EDF=360°-90°-90°-120°=60°;
故答案为:60°.
点评 本题考查了平行四边形的性质、四边形内角和定理;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
19. 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 1.4 |
17.已知关于x的一元二次方程x2-x-1=0的两根分别为x1、x2,则|x1-x2|的值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 1+$\sqrt{5}$ |
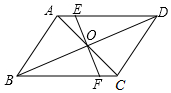 如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.