题目内容
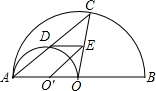 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列四个结论:①点D为AC的中点;②S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列四个结论:①点D为AC的中点;②S△O′OE=| 1 |
| 2 |
考点:圆的综合题
专题:
分析:连接OD,可知OD⊥AC,且OA=OC,所以有D为AC中点,可判断①③;
利用中位线定理可知O′E=
AC,由相似三角形的面积比等于相似比的平方可判断②;
利用反证法来判断④,即如果四边形O′DEO是菱形,则有AC=AO,但由题目条件并不一定满足该条件,可判断④的正确性.
利用中位线定理可知O′E=
| 1 |
| 2 |
利用反证法来判断④,即如果四边形O′DEO是菱形,则有AC=AO,但由题目条件并不一定满足该条件,可判断④的正确性.
解答: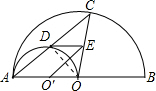 解:连接OD,
解:连接OD,
∵AO为⊙O′的直径,
∴∠ADO=90°,
∴OD⊥AC,
∵OA=OC,
∴D为AC的中点,即AC=2AD,
∴①③正确;
∵O′E∥AC,O′为AO中点,
∴△OO′E∽△OAC,且
=
,
∴
=(
)2=
,即S△O′OE=
S△AOC,
∴②不正确;
当四边形O′DEO是菱形时,则O′E=AO′=
AC=
AO,
则有AC=AO,
由题可知该条件不一定成立,
∴④不正确;
综上可知正确的为①③,
故答案为:①③.
 解:连接OD,
解:连接OD,∵AO为⊙O′的直径,
∴∠ADO=90°,
∴OD⊥AC,
∵OA=OC,
∴D为AC的中点,即AC=2AD,
∴①③正确;
∵O′E∥AC,O′为AO中点,
∴△OO′E∽△OAC,且
| O′E |
| AC |
| 1 |
| 2 |
∴
| S△O′OE |
| S△AOC |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴②不正确;
当四边形O′DEO是菱形时,则O′E=AO′=
| 1 |
| 2 |
| 1 |
| 2 |
则有AC=AO,
由题可知该条件不一定成立,
∴④不正确;
综上可知正确的为①③,
故答案为:①③.
点评:本题主要考查圆周角定理及等腰三角形的性质、相似三角形的判定和性质、菱形的性质的综合应用,在解决有关圆的问题时注意利用半径相等这一隐含条件,有关不成立的结论可以采用逆推法,即从结论入手看是否能找到所需要的条件.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
下列方程中,是一元二次方程的是( )
| A、x+3=0 | ||
| B、x2-3y=0 | ||
| C、(x+3)(x-3)=1 | ||
D、x-
|
 如图所示,C是⊙O上一点,O是圆心,若∠AOB=80°,则∠ACB=( )
如图所示,C是⊙O上一点,O是圆心,若∠AOB=80°,则∠ACB=( )| A、20° | B、30° |
| C、40° | D、50° |
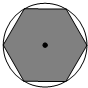 如图,正六边形内接于⊙O,⊙O的直径为2分米,若在这个圆面上随意抛一粒豆子,则豆子落在正六边形内的概率是( )
如图,正六边形内接于⊙O,⊙O的直径为2分米,若在这个圆面上随意抛一粒豆子,则豆子落在正六边形内的概率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
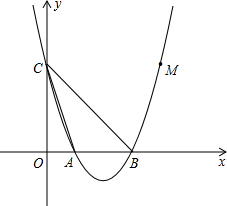 如图,已知抛物线y=a(x-1)(x-3)与x轴从左至右分别交于A、B两点,与y轴交于点C,且抛物线过点M(4,3),连接AC、BC.
如图,已知抛物线y=a(x-1)(x-3)与x轴从左至右分别交于A、B两点,与y轴交于点C,且抛物线过点M(4,3),连接AC、BC.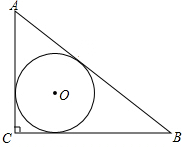 如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为5,4,3,求△ABC的内切圆的半径r.
如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为5,4,3,求△ABC的内切圆的半径r. 如图,在3×3的方格网中,连接AB、BC、CA,请观察并度量∠1、∠2、…、∠6,然后回答下列问题:
如图,在3×3的方格网中,连接AB、BC、CA,请观察并度量∠1、∠2、…、∠6,然后回答下列问题: