题目内容
若(2x2-x-1)3=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6,求a1+a3+a5,a2+a4+a6的值.
考点:代数式求值
专题:
分析:利用赋值法,令x=0可求得a0,再分别令x=1和-1代入可求解.
解答:解:
令x=0可得:a0=-1,
令x=1可得:a0+a1+a2+a3+a4+a5+a6=0①,
令x=-1可得:a0-a1+a2-a3+a4-a5+a6=8②
①+②可得:2(a0+a2+a4+a6)=8,解得a0+a2+a4+a6=4,所以a2+a4+a6=5,
代入①可得:4+a1+a3+a5=0,所以a1+a3+a5=-4.
令x=0可得:a0=-1,
令x=1可得:a0+a1+a2+a3+a4+a5+a6=0①,
令x=-1可得:a0-a1+a2-a3+a4-a5+a6=8②
①+②可得:2(a0+a2+a4+a6)=8,解得a0+a2+a4+a6=4,所以a2+a4+a6=5,
代入①可得:4+a1+a3+a5=0,所以a1+a3+a5=-4.
点评:本题主要考查代数式求值,利用赋值法求值时注意字母取值的技巧.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
下列运算正确的是( )
| A、a3-a2=a |
| B、a6÷a2=a3 |
| C、(a-b)2=a2-b2 |
| D、(-3a)3=-27a3 |
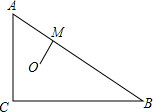 如图,△ABC中,∠C=90°,AC=6,BC=8,O为△ABC的内心,OM⊥AB于M,求OM的长.
如图,△ABC中,∠C=90°,AC=6,BC=8,O为△ABC的内心,OM⊥AB于M,求OM的长.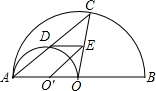 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列四个结论:①点D为AC的中点;②S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列四个结论:①点D为AC的中点;②S△O′OE=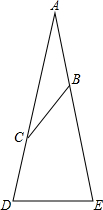 如图,在△ABC中,已知:AB=BC=CD=DE,∠A=20°,求∠E的度数.
如图,在△ABC中,已知:AB=BC=CD=DE,∠A=20°,求∠E的度数.