题目内容
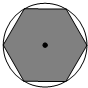 如图,正六边形内接于⊙O,⊙O的直径为2分米,若在这个圆面上随意抛一粒豆子,则豆子落在正六边形内的概率是( )
如图,正六边形内接于⊙O,⊙O的直径为2分米,若在这个圆面上随意抛一粒豆子,则豆子落在正六边形内的概率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概率,正多边形和圆
专题:
分析:首先利用正六边形的性质得出其面积,进而求出豆子落在正六边形内的概率.
解答:解:已知,⊙O的直径为2分米,则半径为1分米,
则面积为π平方分米,空白正六边形为六个边长为1的正三角形,每个三角形面积为:
×1×
=
(平方分米),
则正六边形面积为
平方分米,
所以豆子落在正六边形内的概率是:
.
故选:C.
则面积为π平方分米,空白正六边形为六个边长为1的正三角形,每个三角形面积为:
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
则正六边形面积为
3
| ||
| 2 |
所以豆子落在正六边形内的概率是:
3
| ||
| 2π |
故选:C.
点评:此题考查了圆与正多边形结合的基本运算以及几何概率,利用正六边形的性质求出其面积是解题关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
计算3.14×5.5966+3.14×(-8.5966)的值为( )
| A、9.42 |
| B、-9.42 |
| C、37.68 |
| D、-37.68 |
方程(x-2)2=3(x-2)的解为( )
| A、x=2 |
| B、x=5 |
| C、x1=2,x2=5 |
| D、x1=2,x2=3 |
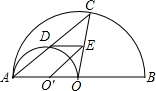 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列四个结论:①点D为AC的中点;②S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列四个结论:①点D为AC的中点;②S△O′OE= 如图,△ABC的一边AB为⊙O的直径,AC是⊙O的切线,且AB=AC,则∠C=
如图,△ABC的一边AB为⊙O的直径,AC是⊙O的切线,且AB=AC,则∠C=