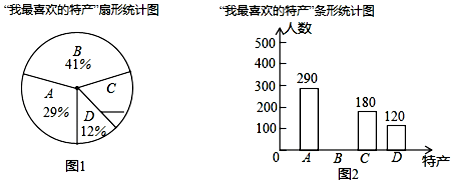
题目内容
4.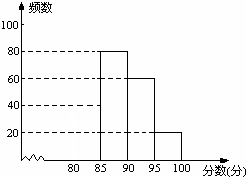 某校组织了一次环保知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次环保知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | 0.4 |
| 90≤x<95 | 60 | b |
| 95≤x<100 | 20 | 0.1 |
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
分析 (1)首先用分数在95≤x<100之间的人数÷频率得到总人数,根据频率=频数÷总数分别计算出a、b、c的值,补全统计图;
(2)根据中位数的定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,结合统计图可得答案,
(3)根据加权平均数公式计算可得平均分.
解答 解:(1)∵总人数为:80÷0.4=200(人),
∴a=200×0.2=40(人),
b=60÷200=0.3,
补全频数分布直方图如图: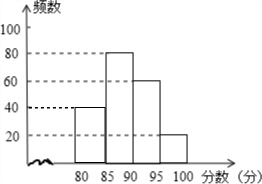
(2)把所用数据从小到大排列,位置处于中间的是第100名和101名,由统计图可以看出第100名和101名成绩落在85≤x<90分数段,
(3)平均分为:$\frac{1}{200}$×(82.5×40+87.5×80+92.5×60+97.5×20)=89(分).
点评 此题主要考查了频数分布直方图,频数分布表,中位数,以及概率公式,读图时要全面细致,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.掌握好概率、中位数、加权平均数的概念.

练习册系列答案
相关题目
15.某班10名学生校服尺寸与对应人数如下表所示:
则这10名学生校服尺寸的中位数为170cm.
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
12.如图1~3,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图6中有6个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S6,则S1+S2+S3+…+S6的值是( )


| A. | π | B. | $\sqrt{2}$π | C. | 1.6π | D. | $\frac{3}{2}$π |
14.一次数学测试,某小组五名同学的成绩如下表(有两个数据被遮盖):
那么被遮盖的两个数据依次是( )
| 组员 | 甲 | 乙 | 丙 | 丁 | 戊 | 方差/分2 | 平均成绩/分 |
| 成绩/分 | 81 | 79 | ■ | 80 | 82 | ■ | 80 |
| A. | 80、2 | B. | 80、10 | C. | 78、2 | D. | 78、10 |