题目内容
如果方程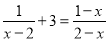
有增根， 那么增根是_______．
x=2
【解析】∵原方程有增根，
∴最简公分母x-2=0，
解得x=2，
故答案为：x=2.
练习册系列答案
相关题目
用配方法把函数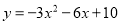
化成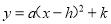
的形式，然后指出它的图象开口方向，对称轴，顶点坐标和最值．
向下，x=-1，（-1，13），最大值13
【解析】试题分析：根据这个函数的二次项系数是-3，配方法变形成的形式，直接可判断出开口方向，对称轴，顶点坐标和最值.
试题解析：∵，
∴开口向下，对称轴x=-1，顶点坐标（-1，13），最大值13． 把抛物线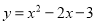
化为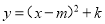
的形式，其中m，k为常数，则m-k=_________
5
【解析】，
∴m=1，k=-4，
∴m-k=1+4=5，
故答案为：5． 与
形状相同的抛物线解析式为（ ）
A. y=
B. 
C. 
D. 
D
【解析】抛物线的形状只与a有关，a相等，形状就相同，∴中，a=2．
故选：D． 若小李做m个零件需用1小时，则他做1个零件需__________小时，做30个零件需_________小时．
【解析】小李做m个零件需用1小时，则他做1个零件需小时，做30个零件需小时，
故答案为： ， . 分式方程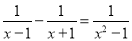
去分母时，两边都乘以________.
(x+1)(x-1))
【解析】∵分式方程 可化为： ，
∴去分母时，方程两边应都乘以： . ―抛物线与x轴的交点是A(－2，0)，B(1，0)，且经过点C(2，8)．
(1)求该抛物线的解析式；
(2)求该抛物线的顶点坐标．
(1) y＝2x2＋2x－4(2)(－，－ )
【解析】分析:（1）因为已知抛物线与x轴两交点坐标，则设交点式y=a(x+2)(x-1，然后把c(2,8代入求出a即可；（2）把（1）中的函数解析式转化为顶点式，可以直接得到答案.
本题解析：
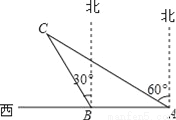
(1)设这个抛物线的解析式为y=ax2＋bx＋c．将A(－2，0)，B(1，0)，C(2，8)三点代入，得解这个方程组，得∴所求抛物线的解析... 如图，某渔船在海面上朝正西方向以20海里/时匀速航行，在A处观测到灯塔C在北偏西60°方向上，航行1小时到达B处，此时观察到灯塔C在北偏西30°方向上，若该船继续向西航行至离灯塔距离最近的位置，求此时渔船到灯塔的距离（结果精确到1海里，参考数据：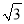 
≈1.732）
17．
【解析】试题分析：过点C作CD⊥AB于点D，则若该船继续向西航行至离灯塔距离最近的位置为CD的长度，利用锐角三角函数关系进行求解即可．
试题解析：如图，过点C作CD⊥AB于点D，
AB=20×1=20（海里），∵∠CAF=60°，∠CBE=30°，∴∠CBA=∠CBE+∠EBA=120°，∠CAB=90°﹣∠CAF=30°，∴∠C=180°﹣∠CBA﹣∠CAB=30°，∴... 如图，在?ABCD中，AB＝4，BC＝6，AC的垂直平分线交AD于点E，则△CDE的周长是( )
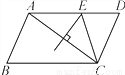
A. 7 B. 10 C. 11 D. 12
B
【解析】试题分析：根据线段垂直平分线的性质可得AE=EC，再根据平行四边形的性质可得DC=AB=4，AD=BC=6，进而可以算出△CDE的周长．
【解析】
∵AC的垂直平分线交AD于E，
∴AE=EC，
∵四边形ABCD是平行四边形，
∴DC=AB=4，AD=BC=6，
∴△CDE的周长为：EC+CD+ED=AD+CD=6+4=10，
故选：B．
...