题目内容
11.小鹏遇到这样一个问题,已知实数a、b(a>0,b>0),请问$\frac{a+b}{2}$-$\sqrt{ab}$是否有最小值,如果有请写出最小值并说明理由.他找不到思路,开始翻阅笔记,发现此题可以用以前老师讲的“配方”来解决
笔记中写到:求x2+6x+9的最小值
步骤如下:x2+6x+9=x2+6x+32=(x+3)2
∵无论x取任意实数,(x+3)2≥0
∴x2+6x+9的最小值是0
(1)小鹏发现代数式a2-2$\sqrt{3}$a+3可以用上面的方法找到最小值,请问最小值是多少,并说明理由;
(2)小鹏通过笔记和问题(1)的方案很快解决了上面的问题,请你完成解答过程.
分析 (1)根据题意和配方法可以解答本题;
(2)根据题意和(1)中的解答可以解答本题.
解答 解:(1)最小值是0,
理由:${a^2}-2\sqrt{3}a+3={a^2}-2\sqrt{3}a+{(\sqrt{3})^2}={(a-\sqrt{3})^2}$,
∵${(a-\sqrt{3})^2}≥0$,
∴${a^2}-2\sqrt{3}a+3$的最小值是0;
(2)最小值是0,
理由:$\frac{a+b}{2}$-$\sqrt{ab}$=$\frac{(\sqrt{a}-\sqrt{b})^{2}+2\sqrt{ab}}{2}-\sqrt{ab}$,
∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,
∴$\frac{(\sqrt{a}-\sqrt{b})^{2}+2\sqrt{ab}}{2}-\sqrt{ab}$≥$\frac{0+2\sqrt{ab}}{2}-\sqrt{ab}$=0,
即$\frac{a+b}{2}$-$\sqrt{ab}$有最小值,最小值是0.
点评 本题考查配方法、非负数的性质,解答本题的关键是明确题意,利用配方法和非负数的性质解答.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
1.一个数的倒数是它的本身,这个数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
3.将有理数$\frac{85}{84}$,$\frac{88}{87}$,$\frac{84}{83}$,$\frac{87}{86}$,$\frac{86}{85}$两两相乘得到10个积,将10个积从大到小顺序排列,排在第5个的积是有理数( )的乘积.
| A. | $\frac{84}{83}$和$\frac{88}{87}$ | B. | $\frac{86}{85}$和$\frac{88}{87}$ | C. | $\frac{85}{84}$和$\frac{87}{86}$ | D. | $\frac{86}{85}$和$\frac{87}{86}$ |
20.已知$\frac{b+c-a}{a}$=$\frac{c+a-b}{b}$=$\frac{a+b-c}{c}$,则$\frac{a+b+c}{a-b+c}$的值为( )
| A. | 3 | B. | 0 | C. | 0或3 | D. | 非上述答案 |
1.已知∠α=35°12′,则∠α的补角的度数是( )
| A. | 54°88′ | B. | 54°48′ | C. | 144°88′ | D. | 144°48′ |
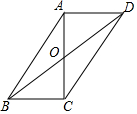 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.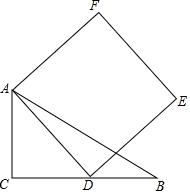 如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.
如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.