题目内容
6.有3张扑克牌,分别是红桃3、红桃4和黑桃5,把牌洗匀后先抽取一张,记下颜色和数字后将牌放回,洗匀后再抽取一张,则两次抽得相同颜色的概率是多少?分析 红桃3、红桃4和黑桃5分别用A、B、C表示,画出树状图,展示所有9种等可能的结果数,找出两次抽得相同颜色的结果数,然后利用概率公式求解.
解答 解:画树状图:红桃3、红桃4和黑桃5分别用A、B、C表示,
共有9种等可能的结果数,其中两次抽得相同颜色的结果数为5种,
所有两次抽得相同颜色的概率=$\frac{5}{9}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求事件A或B的概率.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
17.函数y=$\frac{\sqrt{x-1}}{{x}^{2}-4}$中自变量x的取值范围是( )
| A. | x≥1 | B. | x≥1且x≠±2 | C. | x≠±2 | D. | x≥1且x≠2 |
14.已知某等腰三角形两边长长分别为1,2,则周长为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 4或5 |
11. 某银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).下面是这次调查统计得到的频数分布表和频数分布直方图.
某银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).下面是这次调查统计得到的频数分布表和频数分布直方图.
(1)在上表中填写所缺数据;
(2)补全频数分布直方图;
(3)据调查顾客对服务质量的满意程度与所用时间t的关系如下:
请结合频数分布表和频数分布直方图回答:本次调查中,处于中位数的顾客对服务质量的满意程度为基本满意,用以上调查结果来判断该银行全天的服务水平合理吗?为什么?
 某银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).下面是这次调查统计得到的频数分布表和频数分布直方图.
某银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).下面是这次调查统计得到的频数分布表和频数分布直方图.| 分组 | 频数 | 频率 | |
| 一组 | 0<t≤5 | 10 | 0.1 |
| 二组 | 5<t≤10 | 30 | 0.3 |
| 三组 | 10<t≤15 | 25 | 0.25 |
| 四组 | 15<t≤20 | 20 | 0.2 |
| 五组 | 20<t≤25 | 15 | 0.15 |
| 合计 | 1.00 | ||
(2)补全频数分布直方图;
(3)据调查顾客对服务质量的满意程度与所用时间t的关系如下:
| 所用时间t | 顾客满意程度 |
| 0<t≤10 | 比较满意 |
| 10<t≤15 | 基本满意 |
| t>15 | 比较差 |
18.方程组$\left\{\begin{array}{l}{x-y=0}\\{x+y=2}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
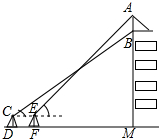 为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.
为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.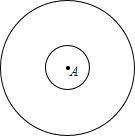 如图,大圆半径为6,小圆半径为2,在如图所示的圆形区域中,随机撒一把豆子,多次重复这个实验,若把“豆子落在小圆区域A中”记作事件W,请估计事件W的概率P(W)的值$\frac{1}{9}$.
如图,大圆半径为6,小圆半径为2,在如图所示的圆形区域中,随机撒一把豆子,多次重复这个实验,若把“豆子落在小圆区域A中”记作事件W,请估计事件W的概率P(W)的值$\frac{1}{9}$.
 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )